Пояс роговского своими руками

2 Схемы

Принципиальные электросхемы, подключение устройств и распиновка разъёмов

Самодельная катушка Роговского на ток до 10000 Ампер

Для измерения токов, особенно больших, удобнее не подключать амперметр в разрыв проводов (как в датчиках типа ACS712), а использовать токовые трансформаторы. Например катушку (ещё её называют пояс) Роговского. Представленный для самостоятельной сборки датчик позволяет измерять ток в двух диапазонах: 200 А и 2000 А. Катушка питается от одной батарейки 9 В. Выходное напряжение для диапазона 200 А составляет 10 мВ / А, для диапазона 2000 А — 1 мВ / А. то есть максимум 2 В.

Возможно собрать даже токовую измерительную катушку на 10000 А, которая бы имела выходное напряжение 1 мВ / А, что означает при 10000 А она должна иметь 10 В. Вы можете конечно купить такую катушку, но это очень не дешево. Отсюда идея сделать себе прибор своими руками.

Катушка с интегратором используется для измерения переменного тока без отключения электрической цепи. Она имеет два диапазона: первый с чувствительностью 10 мВ / А и второй 1 мВ / А. Это позволяет измерять токи до 500 А с разрешением 0,1 А и до 5000 А с разрешением 1 А. Катушка должна быть подключена к цифровому мультиметру.

Когда переменный ток протекает через провод электрической цепи, в поясе (катушке) вокруг провода индуцируется напряжение. Значение наведенного напряжения зависит от величины тока, его частоты и размеров катушки. Данная катушка имеет размеры, как показано ниже на чертеже:

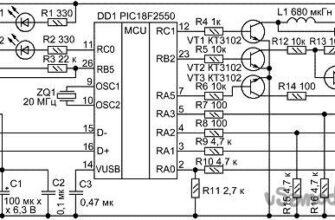
А принципиальная схема катушки Роговского с интегратором показана на следующем рисунке:

Вначале вычислим постоянную катушки в мкВ / А.

А потом можно рассчитать входное сопротивление и емкость интегратора. На схеме присутствуют три резистора R1, R2, R3 и конденсатор C7. Допустим надо получить чувствительность катушки 1 мВ / А (1000 мкВ / А), то есть нужно получить напряжение 1 мВ на выходе усилителя U1A, когда ток 1 А течет через катушку. Усиление интегратора описывается отношениями:

Выбран конденсатор 22 нФ и набор из трех резисторов, дающих в общей сложности 4687,6 Ом. Для диапазона чувствительности 10 мВ / А уменьшим емкость обратной связи в 10 раз и выберем конденсатор 2,2 нФ. Поскольку конденсаторы выполнены с допуском 5%, результирующая емкость на плате создается конденсаторами, обозначенными как C5, C6, C10, C11. На практике вместо резистора 4687,6 Ом установили один резистор 4,7 кОм и нулевые резисторы в других местах. Задача усилителя U1B — сбалансировать входное напряжение дисбаланса. Питание платы амперметра идёт от двух батарей 9 В. Такое высокое напряжение питания необходимо для получения среднеквадратичного напряжения на выходе интегратора 5 В.

Провод между катушкой и цепью интегратора, а также между интегратором и мультиметром, должен быть экранированным. Экран подключен к земле.

Основа — резиновый водопроводный шланг, и на этот шланг мотаем один слой медного провода ПЭЛ-0,5. Самая сложная операция — наматывание катушки на шланг и её закрепление. Она была намотана на прозрачный ПВХ шланг с наружным диаметром 8 мм, 800 витков проволоки диаметром 0,55 мм.

Диаметр проволоки не критичен, вы можете использовать другого сечения. Лучше даже использовать более тонкий провод, чтобы получить больше витков и соответственно более высокое напряжение на выходе катушки. Вид обмотки катушки без внешней термоусадки и с муфтой показан на рисунке.

Катушка должна быть намотана так, чтобы обмотка образовывала один слой. Конец и начало катушки и обмотки заделаны термоусадкой, чтобы обмотка не разматывалась.

В качестве элемента для закрытия катушки использовался пластиковый кабельный ввод PG10, к которому был приклеен один конец катушки. Другой конец после вставки зажимается гайкой.

Электронная схема очень проста и не должна создать проблем при запуске даже у начинающего электронщика. Будьте только внимательны при подключении питания, чтобы не перепутать полюса батареи.

Для настройки и испытаний использовалась калибровочная катушка. Когда через калибровочную катушку протекает ток 1 А, катушка Роговского имеет значение 100 А, а затем выходное напряжение интегратора в зависимости от выбранного диапазона должно составлять 100 мВ или 1 В. Если это напряжение отклоняется от ожидаемого, настройку усилителя следует скорректировать, изменив результирующее сопротивление, создаваемое резисторами R1, R2, R3 для диапазона 1 мВ / A или емкостями C5, C6, C10 для диапазона 10 мВ / A.

Источник

Пояс роговского своими руками

В экспериментальной практике существует необходимость измерения характеристик импульсных токов. В некоторых случаях прямое включение измерительных приборов в электрическую цепь невозможно. Например, в высоковольтных цепях, при быстрых разрядах в газе или если ток образован пучком заряженных частиц в ускорителе. Для того чтобы найти метод бесконтактного измерения параметров импульсного тока, достаточно заметить, что при движении зарядов в окружающем пространстве возникает переменное электромагнитное поле. Регистрируя вторичные эффекты от наведенного поля, можно получить измеряемые данные о параметрах импульса.

Для получения информации о величине и форме импульсного тока по наведенному переменному магнитному полю применяется пояс Роговского. В нашем случае он представляет собой длинный замкнутый соленоид с равномерной намоткой витков. Этот соленоид размещается так, чтобы охватывать измеряемый ток $I_ <1>\left(t\right)$ (рис. 1).

Можно заметить, что пояс представляет собой просто импульсный трансформатор, где первичной обмоткой является проводник с исследуемым током $I_ <1>\left(t\right)$, а вторичной — пояс Роговского. Известно, что трансформатор хорошо передает форму сигнала (в пределах своего рабочего диапазона), если в первичной обмотке течет синусоидальный ток. В случае импульсного тока произвольной формы $I_ <1>\left(t\right)$ задача усложняется и информация о форме импульса во вторичной обмотке может быть утеряна. Форма и величина выходного сигнала с пояса Роговского зависит от временных параметров исследуемого импульса, конструкции пояса и характеристик подключаемой нагрузки. И только в некоторых случаях при определенных соотношениях между параметрами импульсного тока $I_ <1>\left(t\right)$ и пояса Роговского можно по сигналу, снимаемому с пояса, восстановить форму $I_ <1>\left(t\right)$ с помощью достаточно простых методов.

Принцип действия пояса Роговского заключается в следующем. Вокруг переменного тока $I_ <1>\left(t\right)$ создается переменное магнитное поле и создает э.д.с. индукции $E\left(t\right)$ в соленоиде (рис. 1) с коэффициентом взаимной индукции $M$ [2. С. 281]. $$ \cal\left(t\right)=-M\frac <\partial I_<1>\left(t\right)> <\partial \, t>\ \ \ \mbox < (СИ), >\cal\left(t\right)=-M\frac<1> > \frac <\partial I_<1>\left(t\right)> <\partial \, t>\ \ \ \mbox < (СГС),>$$ где $M$ — коэффициент взаимной индукции. Индуктивность соленоида $L=N\cdot M$, где $N$ — число витков [3. П. 51].

Здесь и далее будет использоваться в качестве основной система СИ. При расчетах по формулам в этой системе окончательные численные результаты сразу получаются в практических единицах — вольтах, амперах и пр. [2. С. 370]. Для основных формул приведен также их вид в гауссовой системе единиц. Сопоставление всех формул электродинамики для этих двух систем приведено в [2. С. 668]).

Э.д.с., наводимую на контуре $\varepsilon \left(t\right)$, можно измерить измерительным прибором. Например, если подключить к поясу осциллограф, то на экране будет наблюдаться производная тока. Для получения информации об исследуемом токе $I_ <1>\left(t\right)$ требуется найти метод восстановления $I_ <1>\left(t\right)$ по измеряемой величине $\varepsilon \left(t\right)$ или, другими словами, проинтегрировать $\frac

$. Для этой цели предложено два способа подключения пояса к измерительной цепи. В одном из них пояс работает в режиме интегрирования тока на собственной индуктивности, в другом — в режиме интегрирования тока на внешней емкости. Рассмотрим их подробнее.

Режим интегрирования тока на собственной индуктивности

Подключим к поясу активное нагрузочное сопротивление $R_ <н>$, с которого будем снимать напряжение, возникающее при протекании тока по цепи соленоид. Рассмотрим эквивалентную электрическую схему пояса для такой цепи, изображенную на рис. 2. Здесь $L$ — индуктивность пояса; $C_ <0>$ — его собственная емкость; $r$ — активное сопротивление пояса; $\cal \left(t\right)$ — наведенная э.д.с. индукции в поясе; $R_ <н>$ — активное внешнее нагрузочное сопротивление.

Конструктивно изготовим пояс так, чтобы он обладал малой емкостью. Оценка малости для емкости в схеме на рис. 2 фактически означает, что емкостное сопротивление $C_ <0>$ на характерных частотах $\omega $ сигнала $I_ <1>\left(t\right)$ настолько велико, что оно не шунтирует сигнал на $R_ <н>$ ($C_ <0>$ параллельна $R_ <н>$) и слабо влияет на амплитуду снимаемого с $R_ <н>$ сигнала, т. е. $$ R_ <н>+r\ll \frac<1><\omega C_0>. $$

В этом случае при рассмотрении электрической цепи емкостью $C_ <0>$ можно пренебречь. Отметим, что параметр малости для $C_ <0>$ корректно вводить только вместе с частотой сигнала $\omega $. Тогда, по закону Кирхгофа для такой цепи, можем написать $$ \varepsilon \left(t\right)=L\frac >

+\left(R_ <н>+r\right)I_ <2>=-M\frac >

, $$ где $I_ <2>$ — ток в цепи пояса; $I_ <1>$ — исследуемый импульс тока.

Общее решение этого уравнения, как показывается в курсе дифференциальных уравнений, есть $$ I_ <2>\left(t\right)=\frac<1> e^<-\frac<\tau >> \int \limits_<0>^e^<-\frac<\xi ><\tau >> \varepsilon \left(\xi \right)\, d\xi , $$ где $\tau =\frac$ — характерная постоянная времени интегрирования $LR$ цепочки (см. ч. I, радел 3.1 и 4.1); $\xi $ — переменная интегрирования. На этом этапе нет простого соответствия между $I_ <1>\left(t\right)$ и $I_ <2>\left(t\right)$, т.е. условие малости емкости пояса еще не приводит к желаемому результату. Продолжим поиск дополнительных условий, при которых измеряемый сигнал на $R_ <н>$ был бы пропорционален $I_ <1>\left(t\right)$.

Пусть длительность импульса тока (характерное время изменения тока) $\tau _ <н>$ мала по сравнению с $\tau =\frac$ — собственным временем интегрирования пояса с нагрузкой $R_ <н>$. Полагая для оценок, как и в формуле $R_ <н>+r\ll \frac<1><\omega C_0>,$ $\tau _ <н>\approx \frac<1><\omega >$, можно записать это в виде неравенства $$ C_0(R_ <н>+r) \ll \tau _ <н>. $$

Читайте также:  Перемотка статор генератора своими руками

Фактически это случай малой активной нагрузки по сравнению с индуктивной. Тогда членом $\left(R_ <н>+r\right)I_ <2>$ в уравнении определения $\varepsilon (t)$ можем пренебречь и это уравнение непосредственно интегрируется $$ I_ <2>(t)=\frac<1> \int _<0>^e^<-<\frac<\xi > < \tau >>> \varepsilon \left(\xi \right)\, d\xi =-MI_ <2>\left(t\right) $$ или $$ I_2 (t)=\frac, \ \ \ \mbox < при >\tau _ <н>\ll \tau =\frac +r>. $$

Такой режим работы пояса называют также режимом трансформации тока. Коэффициент трансформации тока $$K_ =\frac=\frac<1>. $$ оказывается таким же, как и для трансформатора с обмотками в $1$ и $\frac<1>$ витков [3. c.136]. Напряжение $U_<вых>$ на нагрузке пояса при этом $$ U_ <вых>=\frac \cdot I_1>. $$

Напряжение на $R_ <н>$ прямо пропорционально $I_<1>(t)$, чего и требовалось достичь.

Дополнительно можно подчеркнуть, что конкретный пояс Роговского с параметрами $C_ <0>$ и $L$ способен правильно регистрировать импульсы тока в некотором диапазоне характерных времен изменения импульса исследуемого тока. Можно сформулировать иначе: для импульсов $\tau _ <н>$ следует подобрать пояс с определенными $C_ <0>$ и $L$. Для оценки эти условия можно выписать, учитывая $R_н+r \ll (\omega C_0) ^<-1>$ и $R_н + r\ll \omega L$, в виде неравенства $$ \left(R_ <н>+r\right)C_ <0>\ll \tau _ <н>\ll \frac +r>. $$ Наличие малой активной нагрузки $R_ <н>$ обуславливает относительно низкую чувствительность $\frac>< I_1(t)>$ этой схемы. С другой стороны, требование малости $R_ <н>$ и $C_<0>$ обуславливает максимально широкий частотный диапазон измерений для данного пояса. Основную погрешность в измерении формы импульса $I_ <1>\left(t\right)$ дает конечная величина постоянной времени $\tau $ пояса. Емкостью $C_ <0>$ в уравнениях пренебречь легко, однако на практике нельзя изготовить пояс без емкости. Взглянув на схему, можно увидеть, что индуктивность пояса $L$ и емкость $C_ <0>$ образуют колебательный $LC_ <0>$ контур с затуханием на собственном сопротивлении провода обмотки пояса (см. ч. I, радел 4.1). Поэтому при регистрации самых коротких импульсов на фоне сигнала пропорционального $I_ <1>\left(t\right)$ могут наблюдаться собственные затухающие колебания $LC_ <0>$ контура, и картина, наблюдаемая на осциллографе, будет сложнее, чем описываемая уравнением $ U_ <вых>=\frac \cdot I_1>. $ Этот случай наблюдается на поясах в данной лабораторной работе.

Если в качестве нагрузки включить большое сопротивление ($R_ <н>\gg L\omega $), то в этом случае пояс Роговского можно использовать для измерений в режиме интегрирования тока на внешней емкости.

Режим интегрирования тока на внешней емкости

Схема включения пояса в этом режиме изображена на рис. 3. К обмоткам пояса в качестве нагрузки подключается интегрирующая $R_ <н>C_ <н>$ цепочка, которая интегрирует ток$I_ <2>\left(t\right)$ (см. ч. I, радел 3.1).

Здесь $L$ — индуктивность пояса; $C_ <0>$ — его собственная емкость; $r$ — активное сопротивление пояса; $\varepsilon \left(t\right)$ — наведенная э.д.с. индукции в поясе; $R_ <н>$ — активное внешнее нагрузочное сопротивление; $C_ <н>$ — внешняя нагрузочная емкость.

Для восстановления формы исходного тока $I_ <1>\left(t\right)$ измеряемый сигнал снимается с емкости $C_ <н>$. Рассмотрим подробнее работу пояса в данной схеме. Индуктивность пояса вместе с элементами интегрирующей цепочки представляет собой колебательный контур с затуханием, последовательно с которым включена внешняя э.д.с. $\varepsilon \left(t\right)$. Собственной емкостью пояса $C_ <0>$ пренебрегаем. Аналогично $$ \varepsilon \left(t\right)=L\frac >

+\left(R_ <н>+r\right)I_ <2>=-M\frac >

, $$ можем записать уравнение для замкнутой цепи \begin \label \varepsilon \left(t\right)=L\frac >

+\frac<1> > \int I_ <2>dt+\left(R_ <н>+r\right)I_ <2>=-M\frac \left(t\right)>

, \end где $I_ <2>$ — ток в цепи пояса; $I_ <1>$ — исследуемый импульс тока.

Подберем параметры интегрирующей цепочки так, чтобы при протекании тока $I_ <2>\left(t\right)$ с характерным временем $\tau _ <н>$ по цепи пояса основное падение напряжения падало на активном сопротивлении $R_ <н>+r$ пояса. Это соответствует требованию малости величины индуктивного импеданса пояса $\omega L\ll R_ <н>+r$ и емкостного сопротивления $(\omega C_н)^<-1>\ll R_ <н>+r$ (при $\omega \approx \tau _<н>^ <-1>$) на характерных частотах исследуемого импульса тока. Одновременно это также требование малости $\tau _ <н>$ по сравнению с временем $\tau $ интегрирования $R_ <н>C_ <н>$ цепочки $\tau =\left(R_ <н>+r\right)C_ <н>$. При таких условиях последнее уравнение преобразуется в \begin \varepsilon \left(t\right)=\left(R_ <н>+r\right)I_ <2>\left(t\right)=-M\frac

, \end из которого находим зависимость $I_ <1>\left(t\right)$ от $I_ <2>\left(t\right)$ \begin \label I_ <1>\left(t\right)=-\frac +r> \int I_ <2>\left(t\right)dt , \end

Рассмотрим напряжение $U_ <н>$ на емкости $C_ <н>$ с выхода интегрирующей цепочки, смысл использования которой и состоял в том, чтобы проинтегрировать $\varepsilon \left(t\right)$ и получить в явном виде $I_ <1>\left(t\right)$ \begin \label U_ \left(t\right)=\frac<1> \int I_ <2>\left(t\right)dt . \end Сравнивая последние выражения получаем \begin \label I_ <1>\left(t\right)=-\frac <\left(R_<н>+r\right)C> U_ \left(t\right)=-\frac <\left(R_<н>+r\right)C> N\cdot U_ \left(t\right). \end

Читайте также:  Как сшить матрасик для коляски своими руками

Итак, получена явная и прямая зависимость измеряемого сигнала с пояса от формы исследуемого импульсного тока, что и являлось конечной целью. Зная параметры пояса и интегрирующей цепочки $R_<н>$, $r$, $C_ <н>$, $L$, $N$, можно по напряжению на конденсаторе определить амплитуду $I_ <0>\left(t\right)$. Условия работы пояса в этом режиме можно оценить неравенством \begin \frac +r> \ll \tau _ <н>\ll \left(R_ <н>+r\right)C_ <н>. \end

Особенности работы пояса Роговского

Величина напряжения на выходе пояса $U_ <вых>=\frac \cdot I_1> $ или интегрирующей цепочки $U_ \left(t\right)=\frac<1> \int I_ <2>\left(t\right)dt $ не зависит от положения проводника с током или пучка частиц внутри пояса. Достаточно, чтобы пояс охватывал измеряемый ток. Это утверждение справедливо для сравнительно медленного изменения импульса тока во времени. Если импульс достаточно короткий и ось пояса не совпадает с проводником, с током, то вследствие конечной скорости распространения электромагнитной волны разные участки пояса будут взаимодействовать с ней в разные моменты времени. Это приведет к искажению формы сигнала.

Вследствие конечного времени распространения сигнала вдоль пояса значение э.д.с. индукции связана со значением $\frac

$ не только в данный момент времени, но и в некотором промежутке, равном времени распространения сигнала вдоль пояса. Если длительность измеряемого импульса сравнима с временем распространения, то будут наблюдаться искажения формы импульса.

Для регистрации импульсов большой длительности в режиме интегрирования тока на собственной индуктивности можно увеличивать величину индуктивности пояса. Это достигается увеличением площади сечения обмотки, числа витков и (там, где это возможно) применением сердечника с большой магнитной проницаемостью. Так, один из поясов в лабораторной работе намотан на ферромагнитном кольце.

Пояс можно намотать на длинный гибкий ремень и «опоясать» им часть установки (просматривается происхождение термина «пояс»).

При измерении пояс не обязательно должен представлять собой замкнутый соленоид. Принцип работы пояса при этом не меняется, но количественные данные, снимаемые с выходной нагрузки, потребуют дополнительной калибровки.

Используемые электриками «токоизмерительные клещи» представляют собой откалиброванный для промышленной сети пояс Роговского.

Пояс с соединенными концами представляет из себя «виток» провода в плоскости тора. Если присутствует постороннее переменное магнитное поле, пронизывающее эту плоскость, то на концах пояса появится дополнительная неконтролируемая э.д.с.. Кроме того, импульсный ток, проходящий по соленоиду, наводит в нем дополнительную э.д.с. самоиндукции. Учесть эти дополнительные неконтролируемые эффекты довольно трудно. Зато существует способ их исключить. Для этого достаточно от одного конца соленоида пропустить внутри соленоида обратный виток к другому концу и снимать сигнал с них (рис. 1). Этот обратный виток вызывает такую же по величине, но обратную по знаку э.д.с., как паразитную и самоиндукции. Таким образом, неконтролируемые эффекты автоматически компенсируются.

Если длина пояса гораздо больше его поперечных размеров, то он представляет собой коаксиальную электрическую линию. Обмотка пояса играет роль внешнего проводника, а обратный виток – роль центральной жилы. В этом случае при регистрации коротких импульсов во избежание многократных отражений от концов пояса сопротивление нагрузки стараются согласовать с волновым сопротивлением линии (которое вычисляется как $\sqrt <\frac LC>$, где $L$ и $C$ — удельная индуктивность и емкость на единицу длины линии). Индуктивность и емкость пояса нельзя представлять в виде сосредоточенных параметров $L$ и $C_<0>$, как это сделано на рис. 2 и 3, а следует рассматривать удельные величины на единицу длины пояса. При правильном изготовлении пояса и согласованной нагрузке собственные колебания пояса могут быть сильно подавлены.

Описание экспериментальной установки

Установка для измерения параметров импульсного тока с помощью пояса Роговского состоит из двух вариантов конструкции пояса Роговского, генератора прямоугольных импульсов, осциллографа и различных нагрузок, подсоединяемых к выходу пояса. Принципиальная электрическая схема установки приведена на рисунке:

Для создания импульсов тока $I_ <1>\left(t\right)$ в данной работе обычно установлен генератор прямоугольных импульсов, выход которого согласован на нагрузку $50$Ом. От генератора на проводник, проходящий по оси двух поясов, подается прямоугольный импульс. Этот проводник нагружен на сопротивление $50$Ом, к которому подключается один из входов осциллографа для наблюдения за параметрами импульса генератора. Если в работе используется другой генератор, то нагрузку $50$Ом следует заменить на согласованную с генератором. К выходу пояса можно подключать различные варианты нагрузок для реализации работы пояса в режиме интегрирования тока на собственной индуктивности или режиме интегрирования тока на внешней емкости. Сигнал с этой нагрузки подается на второй вход осциллографа, на котором наблюдается форма импульса с интегрирующих $RL$ — ($ U_ <вых>=R_ <н>\cdot I_1(t)N^ <-1>$) или $RC$ — $$ I_ <1>\left(t\right)=-\frac <\left(R_<н>+r\right)C> U_ \left(t\right)=-\frac <\left(R_<н>+r\right)C> N\cdot U_ \left(t\right) $$ цепочек. Собственное активное сопротивление проводов r в лабораторных поясах мало и им можно пренебречь в соответствующих формулах.

Источник