- Опоры для корпуса изготовление и монтаж
- 25. Опоры
- Подставка под модель корабля своими руками
- Изготовление поверхностей, подставок и держателей для моделей кораблей
- Подставка под модель корабля своими руками
- Часть 4. Варианты держателей для моделей кораблей. КРЮЧОК.
- Подставка под модель корабля своими руками
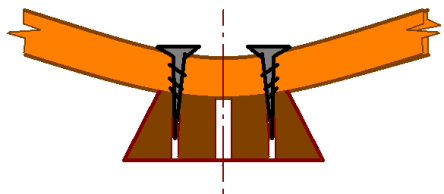
Опоры для корпуса
изготовление и монтаж
| СОДЕРЖАНИЕ |
Есть в сети видео как сделать морской аквариум из эпоксидной смолы. ИНОГДА ЧТО БЫ ПРОСЛАВИТЬ СВОЕ ИМЯ В ВЕКАХ, Спасибо за существенные и дельные советы! Действительно есть работы авторов, которые восхищают мастерством технологии и воплощением художественного замысла. Мне очень нравятся работы Южно-Корейского моделиста Вон Ху Лиая [img]data:image/png;base64,iVBORw0KGgoAAAANSUhEUgAAAKYAAABqCAYAAAA2oiq4AAAgAElEQVR4AYS9B4xld3be+bvh3ZdD5Ry6qnNuhmYzNJNIijPkzJDSaEYaWSNZWksyDAMGFgsYXmExXmOxxi4WhtbwWl7bg7VlKI1mpB1NHpJDchiaodnsUB0r56pXr14ONy/O/1aRlHYXrgH7Vb33bv7+J3znO2e0XC4X4vv4jkMilVT/1as14okEhUKeIAgJggBN00AHYjq+46K5Pl/75a/xL/7nf8lubZft7U22tjb55//iGyzfucHzD58la5n0pnvJpXIYCZ1W0KZa2aVWrRP6OlbcIJeNofkxyo0OzYaNEbhoRgixFLYWw9F1XM/BCDxinotlaARGiK6HZCwD3QtwbIcYOmUn5M07i8yuVdBiSSwDEpbPdFcXPSHkTZ+2brGWyPLU889id+roYchQ/yCZfJ56q4Vju/zxH/8Jc0tr5Ao9mDGDfMbCbzXpyeUJNY/BoSHGhkYZHh0mo3m01jbYWt+kVC/RNzrJjz+8xVyxgqkFhD6YZgzDMPACFy908X0NQzPQ/JBsJkN3fz+prj4CXSf0AzQ8QjrEYinKu1XsjkffwACO3+Ths8f53d/6OjMfX+M7f/09Dp44zu//7j9AHg8E6BjomoGuG4SE8qb60QxTPUN5x9cC9MBAR4+eq6btfRbu7Qd0XUfXdPXMA4JoH9FB0EINLXorel8dGdCI9hcdkujwIWEYvR9trhGGAWEQndveLtXGqVSKr3z1l/nRj36InC1+GKLFDNwwwG02MRNx/DCgXK1iWZb6T9M1Kru76IZGNpej2e5QazdxAg8tptM31E+tUeXwkSOsLyyyvFZhrCdJJmZixlwcJ2Rzd5darYFuJKjUPGzHYag7Qz6VZavapFytMT7UTyxpcvPuEi1XY7NSJWbAYC5HzHcoZCy6e7IYcbnxBr4ORtxEQyNoNEgAoeYTYjOUy5E3dVKuRzqTIGg26M9nWSiWKO2UeeqJRzBMHblHd27PYlkx+vv7uXjxInMLf8ruzhYDw8Nsl5uM9OQ5c2iK0sYmM9duEwY6ftxkJJPE0iBt6cR6+inVWqxvbOL4AoCQmBlDnqJuGCRiFq5v4JtgaApCuL7L2to6+k6FTD5HPpvHNEw838KzQywjT6E/pcDW7LTQ9BS2C7V2m5ZjE7dSaFoM33fRNAM0uR4BqPwq/woodMEMgSAkekOBVoAr78hn4d5noQK4/B0gvwsIPwtw2Vz+FlCrDdXf0W7l30+M2N5x5EvR9vKvBmGEaLVv9azkvWhB7B9bNjXVScmBdB3LNBXK246D53mYho4fBOqCYrEY6XQaQwPfdam3GlQaNdzQJ9AF3AGjkxO88OKLrK6tcPvqdeLmKFBj+946mw2fe2trZC2LA0P9DHZ1Edc7ZPUWZw8cYGa5jmN3CMIGSavAuZOHCLQ4vqYRGiGh75DSIWmGxA1ot1rq3DRDl7uhLE3gtulOWqTiFvWOI8adpGmQNhMUcjkCHHKJGNlEgh//5BXS6SSnTh1nYWEZzwtIZ7K4gcfZ+85xfuYOlz+6QqvZwvEC4kaM5naRgqbTk86yfHeWna01rrZaPH7qOAOFHJqZ5fadWRquS0w38f0AzBDPcwgCn0QiQTyewPF8ZY0M3VAWKRVLoOmWIAfbsTGzMVKppPIEAS6e38F3QrKpDMdPnqXh+Ow227hhSCxuCfLwA3m4IeiR9RO7qwXRc5UH7QkgxALKd/bRqECr4KSsWgQ0Pfo4DAmDAF3t7/9tCUPZj/rZQ7KCXXRseVt52P1vyDPcWwByrrII1NbRilC/yzve3vvytrm/E7mI0PaQBy0g1A2dwPPVrmUVyIqv1qroYUA8kaS/t492o6msk27paF5MuSfDMBkYHGbu+hxWaJG2fPr7C/SODjExPknKMilk4wz0ZFiZm2EgadGfiDHv2oSuh2Ul6Ct0Y5gJOo6PbdsEuo+WsEglEiRiBnarTTqhEdPA8R1anbay+lbSIpvy6E0msN2A9d0axVjIaLZAX1eBgYEhHD+g4pepNDr8yV98i6e2Hmd4cJRE0sJxHbx6QCad4cJDD3D12jUatTqFTILeZJwDE1O89tNXieezPH/ffVTrVTY21nDdDoFn0Ww0ubm0gm/qKkQQq+PYNoYprjWg1QxIpQ3lcZKZjLLyYeATahqGHseKJ9DiMfzAx/VckqkkQbNJtVZip1TiwkMPceLsSSqVXcqNNi6QzqTQDDEeboSrMMTQzMh97gFD3GagBRhiVSK/qoDjh746BwGReERByL7l3PfpyrKpzSIgKsCpr0YAk40iECo/rraXv/dhq05BALd3XPW3tme9xcXLG5pGIO/JH+oNAWYY4oeQSCTJWEk02Ymh03LatIKOskqC3rpywRa6FuJ4Hq2OQ6vdwfdCdNNQaHd9n6kjh3nmiafodkJobHLicDcd36fZ0vG9bkILMukkCcugns3S09NHy7CIZwv0thwG83m683mcwMRIGMT8Or7bIHRk4djUmz6e42ISEBLgqZjMxPc84sk0ibRHLmvQ8AwyqS6arSY7TYedZpuJ4UEWt0sslnYxMjlqtTpvvnmJF194MbIkBORyORy7zfDoCIWeHpydElndYDCbp5DN0dPTw/DgML3JJMP5HD3pJHboMb+ySXf3AOO5DI4cr9VG08VthQpo0QPRaTZadFyXbBDSXejB0GM4nkvb7mB7Hnmri3QiDZpBp93GDzTSqTypRJYnn3yCuKXh2i0cx1GuOpmW4CV60BLOiJUT6yMLQbxgBJAQdSpIriDxY/T05TNldPZc/j4q9sGpABcqQx5ZWbXfffTsA1KOvneUzwA7AquCrQKePCv1I1/di0WjrSJgqtBDTm7vTVO+pWsaHcfGtW3cjh25mZgExlHgGgYGVsyk43hqdcdMk2arge0HuK5P3EwgtyAWsxgcGubIsYOszbxP3h8mGTMwdRfHdAhCT8WLXqtCo2LTn0kRT1hoiRhWwqInk6BV3qZi6WS6ukjFssR1Cx+xgC6dTgfP6ajV1/FcnNDHkPBDxVYhpm6RSaToyjTQTZ1cKktx3SGha+RiHoYeMre1q2LXuG0TMxMUi2U++PAjnv/cL6CFLp7rqAc7NDjM4FA/a+vrhNk0xeou84s+T5y/j9JmUSVhtdouzU6D3rFJenoHcatlHjp4gK7CID+5chU39FRIJQmNWC1ZkOlMDsMycDyH3VKJbCql3HZWEk2JkwOXnZ06HS9QcajEcrl0hoOHJ7j/gbOEvljEGHg+pmkQTyeVEw1VLCgYETMUqAes4m5x4WJFBQ0qjtx/+ALfT8El1l1iUcHDPjDVq8KT7CkC0GcNX4Q0hbto1/tv/H++7i8GFWkq/O1bUTGGAuQoIo42Vq5crkLAmc9m8FNxdNNUMZdhxmjbNl4AVjIFfpNYzCBmWmSzhlq1Yqkke1M71nT1IBLZLOVmlXTgofsmbc9RFi2hacQCkxiaclNi+eK6TsowyVpJ3GSadsejslMmZgVkM2CFKdCzmPE2RqgT00xarTa+ANN3MQJU2CHBvyyOdMyikExh6g5Ou8JUf46xrhw5w2G30WJ5q4Kmm8QNE92QxMTgzt279PZ188gj53F8DwOP9z/8kI31TXWXNmoVUuU4getIyMjU4BCNTou1Spmy3eHO1asUkjmGUynWS7u8c3cOW/dRN04y2L24Sqy3uM/uni4KmQytlkextINRMUikU4R6dF9MK0HaipOIJ5QFbFRrJNMSd8YIfMmWLQXQuBUjmU5FSY1KKsQl658Aaz8RkeN7WgQIgYeKDxVIo1hQABKdo2B3j4HZA9f+uUeGbg9ce+iM/tpH4Z4p3PtzH9zKTQd7Cc/eMfdeFJj3j61A+YkJFVeuFpIA06DQVcBxOmhWjEbLpt1yaDsBpmHgdDx0T1NxZTwfJ6EloOPjdlzCfBRTyKqVo/UPjPDCS1/h3W//KXWJsQzoSiVJWRYJw1LupFzZVUlB0jLRQ4NkIoMRq5EMQjzHY21phe6egK58n9qnJGOh56mA3pQbHQq1YmALICVAl+zclCTMIJtKE4Y6BcuiO5FU1jKVzvDBfIlix8aIC7kUAUZcaWiGvP/BFUXLeH6blZUVNjY2FFUmDzoIDRY3ylSzDquVOleX17CSCQ6fOMlQMkvt3ixe3GLHMND7h2jO3EbTDUX/aJLd7t1wsVBtx2Nrq0hvD/QNjtJNDKHnGvUammlgxHy0mAAlxHE7mLqhXiUp8tR+fBy3iet1VMZvWXE831P3SLJ5OV8JzT4FhtjAyEp+YiH3Pt8HnWBJfo/8aARsCQOi9/aBF+1T9hHRTAIlOSG5PnmNYPp3t9nfWhbJ3/35dLvI0Qs7tP+j0nANE8fxqdfqxCwTrdVmvCePnaxTdeoEuoFmaCSz3WRSvbhuQKOyi+mHuB0HTTOVGwSfQCiSZJLTDz7Cx2/+jOrGHP3xDAkzTkxuXKixvV2k3KgzOtir6CfZt4qzHIeUqdPX1U1r1VYZ7tBoh3w2i+Ebis/0PImJfUWzyHXIxUnyEMUmmkrSrFiMhO6S0KE/G6c7k2O+7vHR/Jbi95K6bKgpyxGEkiFrBF7AO+++TxC0lUtT3OOeP9G1mLKyFSdkt91goVzluV98jjIWTz74ONnBSRq1HQYH+8lms7x3Z5b5xQViSQvJqgNXkgyFHUxdxzB0SqUSoWYwMj7FyPg41UqNSq2sjh34gQo7QskGDF3xoNeu32FxaZ2pySFct6muW5Il8V6S/RtGjOL2tsrK+/oHo9hR3RedUJeYUwK76LGre7YHgn0gRSCRz/dduvwehXL7YJHvKJCrXcln8t1PwbT/vf/a6/6x9o8tr5/BpNrcVA9Uhy7LYkgycdcjr/n0VnaJ+w7V0KWZTNJ/5j7ml7dJ5TLU2y65wCIMG+pBmgbYOsR1k1gqzmpxg9e++33u3lthPBXDtl30wFRuutFxWFvfoSudodFw2NxZwWOVWqNJpdrAE0vAJsXdFqaZoN6wCTGJayau08b3dTyV+Hho2v5NlNUt3JcKmUmmIex06DQatIIkmzstXruzrNxuNplErEwYiytw+/hRdB8GmHH5NaHcfCD8bChW2FT0jhmLMm3HDpg+fJjjR05w584dnNDm4LGD/OynixR6+5geHuXv/85/w7/9o3/H5vamWgDRjZfFIMS2RyyRJDR1yqV1WnaViekT9I6MYqQN7EYTceWuWNeWWEWLvv4Bmh2HaqWCrg/iOwIPk1TSIh5L4DoBiZjJytoyhUIXQ0MCXk+yBzSJLoUpQhiX6HErYAgS9kIMQcJnwSK50D5YhBtVcJTMfd+yqlBUYlexlvsU0R7q/2uo3N/H3jH37428Cjr3YS4hE1ZMZyih01fZJXACNMskVUhiBiFtPaBjQrm4Q6xVI/Q6pBJpqn6Tlm1CYJO0NEwrS7m8y1/+p2/x19/5a5buLjCSS1I40ofwdZIkEOhUGnU6HYeGaTM7s8Ly5gaJZBqJZxvNNgLcINAp5AocnhgjkxKz5dP22xB6qmoiJJaK0xXJKxcjN0hXcVSoGyo2c3M57m5WeGPhHrsdh6bjqCpOEDfpSHXEE0pG6BwXTdEmESEuLkyZX3lwwjNKQiJJnmOreC+ZzvLYE0+pjL13cFCR6Q9PTDM1dZQQl3K5xsWLT1KtNvhXf/ivPnng+89L7rdYaNOKKUK/1elw+8Y1pg+6TExNYmcK1GotAl/ucwLT1BRhLoUO9RCDENd1KO0USecTqvjhuFF8vbNTYrC/X9F8cvqR65YsXZIqWcSBimM/STM+iX8jN6vAoTJ1CSU+de/KKir2OyLLBaIRkD8F4z6w5TrVeX5ywRFVtB/v7n8ur7KNYg726aT9bYTHlBslq0rix7SKA0JaTkBMz5JOJ0jYkBT6olok7wds7tZpaWVqrRpeoPOf/9N/4fB9V7BDg7DjszK7QC6Vprevj+3tNeY2Q6YHuzGDiBe1XZtcT4G+/j7CfJaaVEM6DqXijjotKc/F4ily6TSeEdL2HSzhBS0UiR96srL0PVcseayvLk5AJKCUUqWscdf3KNsuq7WWejCWJBaxGHGg1azhScnNjGOapiLnJYmTyogkvMI0CO0idI/t2wqnGjGEDrvv1CmmDh1DNz0V8+2UK6DHOHriBDulDbG/lCpVjh47zsTEGPOzd5Xr9v2IE7ZiAjA5TxMrESeeSNNpuSzeu0fo2xw8fALLSlOuFGkLXeT6Ko6WAoYwBoHvR6+BRzwex7QsRa4LDdVutJGynh84ypLJ3ZGQRcInRVMKOyCGci+UMaRwsW+i9kCxD85PMRJ9JwJqBCZhGParSvvfE5DJtp9sv/e33NPPxpf735PtBJT7n/3dmFZFUXqoETdjxNPqqagLqTkNKqGDrceodzxcXccJNPS+QXK5LEPpuKptv3bpA96ZuYpTt3n+qWf4whdeZGl1gZvXZ+i0mmRNm9Wb10gbcZU1m6ZOJpei4wtxHnJgapKubJ5yqQSBp2gpqeoI2d2yaziOLF3J0C1iQhBLvKSokb1Vq4VInEgY1X4JJVP3cdsttSINCeLFhcaEdoK+7gxnH3uA6zdusrC+i2bEFLVkqBjYwvY6irKR2racg2gFDN0k8ENliU+fOYdmGFGla3xCPViJefPdWbywTb3eYKu0Qy6T4eChg8zP3tmzVntxlCYVNkvxr6YZJ5GO05WLU6vWKG1tYiXTDA5OMjw4wPrmFrYT3ZOOIx4jUKGW02kjxLxoG4RhkJJqW0rJhkkymdjjTZW/jZITZeHk+FEVzxBqRhm7CJUKrMpPRNYtApuALAKisoDKqinvv49F9boPRPnuZ3/kT2W195D/6fci6x15ps9uEf2+vxsFTEP3qRkGm9leMUtoiRReIoeRypHL5pkc6COTy5DLZBG+TU8atDtNPNvFabe5e2sGO2yxsbjA6z/6IYPDwxw/cIALD55l5tpVFmdu0rYbpGNx9JjBVqOGIwIGIdZ1j+3tMgYxbM9habeI7XRIJCyV+ToCskBcuEc+lUbOVVkPqUZJDBhEcZOp4ilHVaJcL6TdkboImGJpxcqKIMS1sVImv/uPfovZa3f4D//+z1gTwt6Mq8xbrKRX28Wnju3Kw997cHj4gcexQycYH5tUNX6psY8MTzA0OIDEn+lsWtFnrUZHJRqFrhxnzt7Ha6+8QuC5KvEQYLTbTXq6ugk1nVazo0Aet0y6enPU6lGpdWNtiWyuQKYrC40mlm7hFKtKtCIJp2e38L0OIrSR5Ch0pQDSVBZUXL5Y9sjCiUWKyivKeqo7EpUaxeJpfkTCRwhUjkFZX1VZ1wWkEUwUcD9DzKvwZu/eRNz8/iKQtbOXfe+BWr67D+x9cEYQjEC//7u8qtLA3ioxpYLw0In7uXj/OULLIJnO0NczSCHXhRWXle0pccb2zhbl0jb3bl6mWN+ltLtDvVyhVqrw8IVH+OqXv0JXdw9TB6d5+733sf2Q5dUtLl25gZbO47QcrMAldH3KTVdZ22JosLC2TnmrQkKV5AxsDRquj6XpETlvwsBAnpQVk5I4UvJUMWEgiYrc7shVSU1fkcxaQLVZV6VMuVixfGJRxVILH6tpCd569wqmA4+ef5L3bi9T1mLoloEWegTOMJ1WjWZDVD0tbKmydJqKzD95+j7MeIJA8zF0TekJJMWQ0CJmJRgZGcXUDKqNqqg0OHbiOAMDg6yvLSt7JGU/AWelUmXq4CHarkO9UVcxbGBZKrMWKiyRjLO0tkJXPUNXoYtGs0EynWSwr4ClB4R2U3mXpBUVNuQ6K7VqVJ4UpHi+ujfyvoQNEUplkQktGLlP8R7CZij6U+g2+XJ0N6PYVFk8AZkAS7aNzl19be970fVE+40spgpMo/gzWtOfgDLa7tN/92PS/Vfl0vfALt8ybdvhwrlT/NN//Dtcm7vL1RszJIM6q7dn2SmXWN1cY3ZhgWqzidNu4XkuXnSbcR2f3/z13+T3fv8fsba2xfziItVmgysfX6G4XeTB+x5ATxeIFwYJ9QCnVlSlMblOKbfVK22SJJg4eJLeTEEunTD06bi24unsoIOWMZTrV3ZRHqzcWD/iM6VSIeGm3FWVqYdCO9nUGjViwilqGsNDw7TtNo1KDZFvbWyWefO9azxw8igThyZJDA9zd6vI5s4Ovm1gZnKYfYN7cZlHXJeyp0Ot2WK3XOPSpXcZHRliZKgPEjFlHWNWHF8qNXvAiyfiNJtNent7OHzkMGurS+pRqjRfqmydDmurq0xMH2B4eIjt4g7tVlu5/Ea1Su/AIF09XWyvLNOu1yEeZ2pqXNX7DZEASugShCQTSYU5ua5Go05vV2bPf0ZYVA9dWaBQ0X2fwkI238vKBUt78aD4Xl0TyO6FHQqu+3HjXlIYQVUBXBaZWEEJDYSDjKzynpXdO5jsW37kXPbjyb9rOfc/V9/c8+WmCDLeufwW/90f3GB9a5utzS2l1mm226oKolRbGEqgkUnFCEOLZsul3Qp56cVf4+WX/x5BoCnieL24yxcfeljVslvNOkPDo/zVD15lY22Vs4dHWC9uY1gBCdNkcKCXQxMJgo6N2/DBbinX6XoS8DfRtYB8Kk6qO4cei5Q6XhAF/rrUx9Vi1pX5V1ZRlDmBTb1dV2qApJXE0GWfOoNdAyT7B1heWafasFlcWOPZp58k393Lxtwcj5yaZmszx/p2idWNGgQmetwiYVpkYjpSgh3s05HErdO22ZpbwmzVyB2fxpBavu1Tt10CTyiqJlpMi+RuIRw/cYLXX30lsiJy00URZBrqIS3MzTM0OsrYxJRK1mrlMqvz8+ysbXDo1CmsmMbm1gZevcPU2BiJeBqntaX2IWqkWDKtYkXRedp2m0xuMEoQI8MVAUwRMJLMRcnGvoUSMIiXEQst6I7eF2jsA/Cz7wk78dnPxGX7ipcWCaTruFTqdQLDlIPsWd9oE9mb/ERgVDfgb1nRfZB+9rzk+6ZkpQtzszirHSwzTlo3kKBcwNCxItcpG7niHjyXZsunkB/g61/7Ks+/8CKvvf0Wma4evMDDiMX48KNrfPTeR7z44vMQi9PT282j5x9kdm4GP1ugUS9haT6JdJow5uF4TWp+i3K9TbvZlutSQX1XKkcqn8cyjCjWC4U2iW6PJ9rDvRsVeoa6wVKerIkUznWIy/n6DqYVZ2JkQlWMUgmTfgdy3XBg6hDf/etXuPDI/XRsEYg4PPv0s6ysr3N7doONYo2tUklpAzTfwDKiWrPEZTErjSyH0laZ6YkOXQmdneougZElZupK39loNEhlMxhWkuPHjyrrt1vaVeyHXIGSnwS+UjHVKmWulN5n8sAkUwcmVRx98+Yt7tyZoXdkmHg9i67ZDPT1KcmhFCJExyqKpVQiiS7KIcdHsv5MOq2ydoVCqYypWriqkhOG4ueMqB6uwCjVWF2R8+J5PsmK92JEgaFUr4SWU8mlUs0J6EIVcsSMuCphJ1Jxqq7E86GiDTuu6AMicCsPKF4t3Duu7kUJkXLZnyZXEXT/9r9KXSSUg5kRhbWcjlSK5TAx4npcJRiSdYoL7dguY8OT/N4//CcMj09TtVuks0mmDoxx7epHPHDuQd55+z3MmMXt2SVe//lbSuM51ttPs+3Qd+AwidDn3uX3yOo2GcMkoSfJ9HXT128qoYHcTnHLlqJURK5lq9KlVDdEbe6K1QwljHJVGVVoHsf1lBrKDzWSulRxbFxTp2W7jHd109eTY2drS9EzUo2xbVGHWyTjKV588fNcev8yr/z8HQUUkehNHxnDD23u3l1ie7PFbkkqMiahZSlxsqWbpHSDj67eU6HLF3/lyxSrLeWOJZSRbH4gm6W70IUZekyMjxEBM9JDihuV5EkkcUMjwxiWye2b19hYXeHM6Qc4f+ERljfWcdvQ3zXKbrCjuF4xj6LlbNmSYAWkk5bSfTodR61Y0XtG7jWyVhIyCQYl9pbqnXg2BcC9GFHK+SpGl/q6gFNxmJ6igiQMiha//BsplrQgICMlXrkuMV54uH5blVAHhnpxOi1azTaK21NBp1gSKZdKCCZAjGJWgZn6+FPb+rdRKXZboCiC4ISpKymZKGwkYpMbp+k+pi4qF5FNhZhGjN/5vX/Ig489yQ9+9gb/8n/71/QOjqNhEYvnsNIF3NDksWeeZfrYcXq7e5kcG1c83ksvfIGjh89ybbZIxSjQCi0lwhX1dyFh0ZvLKLmbaBBTmSRm0gSlLteVzM7TpC0hwPUDHNdHKjD1eodqvUlDLKUnqhtD8X5i30Qp3rZdNosbzM/NcujQNGfOnuLQoSkmpsb53IvPs7S2xvd/8ApXP77Jd7/3Q4x4gvMXzlOvVFQm/MSFB7hwaorHHjhFf08W15HQQDJsHUdPYhtZVrel0ODTcm1qe0mSWDSp7SdFZGGY9Gby6saLIxNQigdSWbGhs76xTjKZ4sJDF1TC9sbrr6sKzujEEEZMMmiXfD7N3MIijY5HYBh07Da6EZJISKlUV+Ji0csKRyo/EtYp1/hJZhwoc2NqPrqUYFVBQTJ3KSJEdXll3cTCiiuW7fahonYmQNLJZbMUCgUsw1QKcylz3rwxw8zHV2lWakpbIV+XkmvgS9xp4esJxRl7St8g1Nb/Xw1ewoM9lyiYlONrgY/hd7CkMiCfiXtQ6buHE4i0Tfpu4jz8+HMks/38+LW38TSLQl8fC0trLC69r+iU9aIkBx8QJpK4nZYikVX22aliJZN0mo7Q4RQGRpge72d25l00u4NhutiNXUWEC7Mi7Rpu4BC4LoYv9W8RkmpK6dRxXBXTSPwvCiNDkzgpuouhIrHFOphU6m16+4e4cP5hSltrLC2tsrG1jWmlOPfA/cSTKe7cWeDWrVl+73f/AY8+9ihXr10lHjeJJzLcuLbAow89wIGJYRw34MTxKe7cu8fla7epNh1CAZtpUhgeVtWqndIuMSNGp+3gdTyVjDiBLWtLVWMUYIyoj0ZaWNqOrZSSP4MAACAASURBVBTt8v6dO7c5efIEjzz8CDdv3mPmxjXWi4sMjk1RLtdp1+pUK0UuXnyIvqyFJ7xzIoNpRoIYqfwost00CQJbxZYiypH4TQBlGiJEjsyUWELxitJf5Mt9FT2uiuk0RGNgBNICJll9pDiTcEAoINGhduUKSq8gOoJOs8kb77zNtZlb2E5AqRkyPNRPqbjFxNgohXwXrY6PZaTBFC/nq4qeUCvCqnxCK6mzjRaSWPv9BaFiX0G355t4oh9Uq1msryQ8ovHQ1IGfef6X+OVf/zof3byj3PTTzz3L1MYkxw8dJXTeZmxinHqzzfbGBtlMilfee4exoWEuPHae//ifvslf/OV3+NLzL/JPfv+3uTM3x5tvvU3FTbFeq1NpVqV7R/FqgYg0AikPiircU8qjmGEpCyT8ZiACWLm16vw05d5FVa9Sc02sgIavW+xWqwRBhnq9pTjNQwenyRa6VYhy9eMbrCyvc+zoURUGSPwsFM5Oscystchv/85vkkhZvHX5bZ586gnmbs7gtps8euE8J48d5OfvXOXqwgad0CIQcUs6gdOxabpNmvW2qrXLyhY6JZ3LMTl9ULlQgYCpxxSFI6AS0j5mSUIZcP36dc6du5+HLjxEd18vt+7MUC/XmZqcplqtqwLE9laR7sQQdlsKCibxPbrIbrdUaVIoq72mA+W2RUTtuG2kVUasuoQOUoJ17Y7q2aq3O3RaNq7jEUsl6O0pMDk6wOjQIPG4Qcf1EUqqp7uPbCanPFUslqBar/M33/8hf/2jH1FzPFxP58b8CvedPILTKNGVfZKx4T4q2+v81Xf+mlx3jt6Bfrp6+skVuskWeoglE1FCJAIasbKq8KDEbupZRuy04aOZkumKa4gpO94JNOrtgNpOk5de/gpf+frfx1FJi3CbLlevXlNZaiabZXljjcASiqRNKpvl4PQ0axtbZLMJrl+7hqVneOzi84oL3Nha58b1W/R2DzA4NMK3v/1nXNndZiiXpS+rqwA/IEEQNj9Z5VJIFALdlNBCBDcSfyoOUzJLOV2JTJUdUFrSRtuj1nEZHs+xsb7OtWuX6epOK9V9T++wAmE+n+XJpx7lvUsf84d/+G/4la9+ib/3W7/BT37yOv/xP/wJZ04dVrTOhx9e59lnnmJjfZmZ2/P0ZNO8/LknmJ7f4Huvva2EzvV2E9dxFLA7HU9pO6uNBl7bJZvNc+jUSfKFgtISyMJJpbNKkd5o1lVbRqErrzoDrl2/pipRgyMjyD43VldVNadvZJLe/mGmpqbx2ru0mw31MJNJk3gspig80ZUurxcpFbepNRqUay0q1Sq1WpV6s0GzZeO5nuJMpbQpSZTkFKLWEu2CUGpmLKQrn+W+U2d57sVnODg1rp6TFYvzwZVrKrFq1Ou8+85b3Ll9k6mJCbL5gqK3hNaaGOxlZOQEtUqV+dlZJaPMjwyRS+dUYi3X880/+rdYZoyu0TG6h8fpmjxMoquLXstgsrtf0W5i1JUXtEOdYgdaHaF9fKUeUp0RbZvHzz/K51/+Ne7ML2LEdcZGR3j30lX+6jt/wwsvfJ67d+dYFpV3LMHayjqVYpF0IsHt2/dodprM37nLs888z8rGFoYV8sY7H/D++x9z9PAxxsd6CHyXatum1hZ31EN/IaZWs5QnxZKIG5L/SWVIwKiHUZAuD1j4O0USC0cmrsfQcTFUZ6VvWpw5fR89fYPUG1VymQJLc9ew2x4XH72oGuauXr2uErqDh4/gB7qyTHa7zcryEo8/9jD/8Pf/Ma+89jO++73vc+bsaYQE36jVydTLHBzJ8WsvPEJhdJy5pRXWN7ag5dOs14glwPMsVZJNZixV1ent7aW8u6vcpFBpIgxJpVMqPizvlBgY6iefTHDj2nUOHTvO2MSYimWXl1cpVWrku/KsbJ6jP5ck19vP8bExVSq9Pb/E9m6NxcUV3nnvspIuttsdpeSSY+iBr/qilLRQrJvcPz1qx/ACm07Q4cjBAzx05gTHpw5QKlfYbnrkhw7hanHaHZ+333qdn7z2Ew5NTdFp1OhOx3j4gZMkEwmGBgZJJiwaGYOR0QHlccu7ZYqlEv3Dozz3pV+mq7tbgVoKFcfPneHKlY/I9QyyvlPn5+9fYeL0aa7Vdkn6t9mUkMiUtppk/ButNqwVPbbrDpW2TVuSC8/n8fMX+Gf/7T9leKCfO7dn6B8a4MbNu4gVmZ4+woUL5xkdHaVWa/LQhYdVVaaQz3H4yAGu3PhY9QI989SjqjvxL//q2ywsLSjVeCKe5eGHH2Zycpgf/uh7tG2JcmLYjstIT46MHkpYghXomOrmiqBCgmqp8UoTilh7qZHJf2IxRT8jgbxJpeMyt1OhFRoM9g+ztrpO0/Z44vGLZDNpRkZHOTB9kNm5OV559ad8/oUvcd+D5/mb73+P9fVN1f8zOTnJK6/+TCmFhkaG2NrZVq7y+ec/R73R5NatmyRNjYmREexOB+EjJeZq1RtUahXi6QRJyyKjacQ9G79e58qV6yytb6i4UC4mk00zMDik7plUpZqtutJddnX1UNwpEk8mGBoaU9I1p1WjO5+grydPf18/BDF6+wd5/6MPefWNt+h0XLa3SqqrUnrsPdcnlYxHFTLNVI1rn/vll/nCC89x5b0P2N4s4rU7pGMGv/LS5/ndr/8aX/3SS5w+c4Jd3yXRVWBjp8mNa1dJGh1uz1wjm0mSipsUZGFkUipGFOlCs15XyaIcd3Vji9tzi2yXqgSGxfDwCK7d5L0rH7JV2qa3K68otA1hA3q6sfHI5sTAtJRhEzbm+jtv0iiVxGJqUT+5EohG1knizEw8wQvPfo5GrcZ8q0VXXx/Xb9zmu9/9MYXuQZ559mmFfJFgieURrd/q6qrqbz734GmmDx6jp6ef0dEDVKq7DPYPkkpYTByYYn5+k3K9xs07lylXaooaEJxV2j6LWxVOjHbLDAZ0VzJGUZALhaEMiIrbJO6NeqcFlVGQLurvju2xUa6hpdJMTR6hu6eHDz/8mCBmcenDD6jsbJFOZ9nZbSixyOkzp9nc2qLZaqsKkRD10g4rMWdxZ5er127w1C8+zfDoED/83vf48//yFzx+8VGcdodKs8H2lRnGhofoMyKg3WvU8UURVW/RMzxB2HborGyqQQ0D+QJ6LIEZjyv6RTxSvmdAGFEa9YqynO1ikUa9o/qfrl65wsT4YV764hfpy8XRNFupjd5/+xLlchvDmmVxdYl4KoObsilt79Df20O7Waenp1spqMbGh1je2ObR557iwtPPcvrAAIdG+/nmv/8mmXwXX//N3+DIoSne++Ay//v/9Z/Rct2YCY2TU0NU1hsM9BVwylscHB/A86OkSBT1lWoZMxZTIZQYE5kHsLO7RbUhJH9etXv0JNPKUsZiULUdXnv153zw0U1OTx3l/Y9vUEnrSsDSk4oTCz1Mt0YiHlcYEe9nJBKJb0gZMPDt6KHvVQGmxqcYHZxUDNbQ2LDKLRaXl3HxVeOaZsSpyQABNeigwcBAHxvrG1R2y0rp8+H7H6pSFYZF3fGZvbfAzmaJju0zNzur+E1RxAiRHCVcYvM0qs22shZd2ZQSK4ir1mMSXwqzEUMa48SFS3lLiFxTNcwFasBAqROystsi1zPA1ORBTp88QafV4JELD9E/2M/i0hp2B97++Vs89fTjPHzxSb717e9Iqyi//rWvUWm3+eY3/4Milj/3whdwHJdXfvRDWs0GJ0+epNXq0N3drZKDmZmbxONphgf7MUxVVpHmbdxOQ5X4RIzc299LKp0j1ZVhbmWZ9z+8oqy7WFQrnSSbyUc1d6el9Kdi6VqNBtVymXwmzW/+xq+pZMRpVFlfXmZhYZ65xUUyhQyra6uqbDo+NK56gKT0V8ilGezLMT7WS3+hwOz8Mjsth2/8iz+gN66xtrTM2Mgov/qrX+KFzz+rBCjCcS5vFfmjP/5zKvUW0wM9pLw6ll0ia4lTkt6uSO+J65FNJugpdNFqe8wurrK2W1GhRNsLSOayqnxMKk9gpTl59DDNapVrtxaYX9lWPVdSKJCGwqW1VXTdYnN1m0bDpuL52CS5fekSjVIxAqbQAxIYR2qSUF3wyy++xLPPPEulWuHyRx9jGHEy+QLdA33slHZ4/c23eO65Z9WDKu1WOHXipKKapFH/woWHWVlbVWIEKY532nVuXL2MHnocOnxMTbc4d+4cgefw7qW3FNcjsjMRFEsmuVuTXhddVTIkQG/7Prb0vQea0k6qwFgqaUKB6BqdQGen47NaadHwIJvrUg1rrY6tGsomJifxgoCOLZ2agSLXu/p60a0UtWpDEeuiD51fmFedi/lcjpPHT7C5VeTtdz/g4PRhHnrwAteuXeeHP/g+UwdGyWXjlHeLnDxxmL6+buxOwNTkpFIzVRplipUyRjzO6PQUI4cn2W02eeWVN1RG7Hmi8dToznep6sn16x+TTKQYGx0jn5dWXYvf/vqv87Vf/xqvvvYzfFF86aYKLbaLJTLJLO1qE7cj2XScan2TYnGRUMju0KXVatDV28WJ0ye574GzZNMpfvLjnzK7sKz+G52YwNNDLn3wPjdnrpIydI6NDPO5Rx6gx9LRXVn4Pq2wo7jkTrOhzlu8onDDiXQXr77xLuV6U4lx7JZHf08/qViM4wcPcf995zl84DC9+ayqLg0ODvLA6ZMcnxjm9LEDTAz1cu7gNKfGx7E8l/pWkdPTR5nuH+fym69S3Fzbt5iiivZUx6DwS2eOnOJ//MY3KHTn+Omrr6oEYWB4iEDT2djaIiblyo5NT28PK8vL3Jq5pYLupaUlZm5dV5m5WLrDh6c4fvwwvd1drK/MMzk5yqEjxymWdlldX1ci2vn5uwqYYn1SqawCj2TapVqdukjXTBMtFlONWjFdIyZ6TKGEDIN2qFHu+KzXOiyV6mzXWxw6epz77ruPiYkJFQ5IY5ZMv/j5u++o+E/c3Be+9EU+uHyFtfVNvvLlryqS+8/+9E84efw4Tzz9NFvFHX726s8YGR/m4i88qjJQSWryXWklnLj42FOcOH6UuXvzLC4s0NNVoFlrUKs3OHxsWjX0CWfatj26e3oZHB3EiFu88fpb1Mq7WGZUCJD6q3irnVKRSrlKp9VWnOn4+Aj/6//yP/HDH7/CRx/PsFOuqzlKfSMjqnBhJZKKh83sLUBT98ikpMUipFl3kQqh4/v8wX//zzh/7iz/5l//a+ZX15TFn5ufp6+/n42lFcrrqwROA9epE7cCfC+qWhmhEWlQbUeJq1VS6QdslHa5JKGRKXV6k7W1efp6C/QP9HPq1AkuPnKeCw/ex6GpCbrSFlYMmp5LNh7j+PQk44N99PcU6O7qor+rh8nhIR48c1K9f/H+s6Rw+cF3/0o1AiqCXSFDKJfAJ5cu8Plf/DwffXRZKYKeee5pxV9tFbd4+92PeOSRx/jeD/9SiW8//ugyx44e4vz5M6TTeSWWLddKqh1gfu4ulVKRWkXaMUK2dnbZLu3SthNsbBbVdA7Juvd/hIPL53uplndljAG+prNVb7PTsNXIl1TCICkuXSI0Xxo0xZJ6KvuURG2fmu0q5LDbDYb6etkt7vLQg/czMTnGTmUXx/GUwCObyZJKJrE7Lp12U2k9R0dHVNlwdFrDSuaothzy3Xkmxwe5+aFJd6Gb+y88yI9//FP+z3/373jp5V9UQ7Xu3bzGyPgIuZ4+Lr15ieKaQX92gMm+JuVajY2lZe6lTRqNGr1dWValUU50lKLKsQwyhRxx6doMNeqNhnLL3d39XJ+ZYbO4jVBK9VoLz3ZwfRsjYdGxbVUl8mSkTqetttVCXdFxDadNPsgyOtTLGz/4ERvFLRrVEj1dWdUSO9o9RG1jnonhIbqH+nBDGffTVImnZ0eiZE+38WSggifJjc1mtcLa5haNRpt6q6NyzxdfeIGnLz7GjRs3aHoh9198jAGpCmlQazoKH9mUxbDRRb2yq6R7uy3RM7ikMhk6oUsiDOlOxjl4+JBKFo2JUfL5nGIuFDBVJVRKKcCXPv8CTzz9JH/+rT/n6LGTnD03wbUbVxQn5no27U6b3u5BxQWuri+RSMWUqDVrt4kr+ZdUYwzOnDpHzDJoyUQ1UbI4AQODgxw6cZypoyGa1+byh8V9XKrXbD6veEhx8dKXIvVbOSuZQ1TvCIj36wJ7pZ69vyVlk594LM5Abw/1Wpn33i8qCqfQk2dpdRkh7o8eOsbV69f4s7/4No8/9rhqo/2j/+Pf8OWv/BIPnX+Av/mbH/PN//hNPvf5z/NLL38BUeAODYwwOj7FBx9dp+2F7FZrbOxWySSynD91gs2lJX7w/Tc4eHCSjt0hbiWVMqqQSuJ3Guhuh/r2jqruzN+9o3rh03paScQ67Q4JyyKXTFMLRfaGas9otJoUeodZWPoexZ2aijePHTumhj64gUapUmJjbUXNb8KXCplOJpWlslvCkWFigz34vs33vvMXNJpN8gO9ZA2dxx5+iEwypVo4EskYxXJZTSpJWnGSRjzSKmiwvVNkQzouidNoOTQ6Np1WnVa7rYjyobExuvoHOXnsBAeP3s/Hq0V+eHmB+Tu3efj0SYS0O3NkSjXMNavS/Wmzu1qEdBbfSLK100BLJ0hrMWYX5+hLxRQ21nebCH8uZIuRSMS/Icy/MO+/9Su/yq9++ZeROQA2PpV6R7m0TCal9IhP/8Kz3Lp5k7nZZZ555hnVE9OstxgaHFPC1e2tTe7cvq1usBlL0NfXy5GjBxgc7FVj+o4cPkK6R4LyWa588B6dTkPN/5H5RKIw7x0YoVat4jrNqMivLOp+Y9TfwvAnf+xDVN44fuQoX/u1X1W1dTGOY5OTjI2Pc+Xja2ocoCwqzYypMOKRRx6lXK6qeUyZbFLFx+J+bafF+QfOqVbc5aVFFbIsLq3yznuXmD40zgtfeFEJOW5euUzMtCk3aqxtlHjisUdZ39pUyYkMjNClmyoWYKWSxOIJau0Wa+LeOy7VaplAKl2GSX9vr2r6263XVesxpqEEyg88eJ4Ak06rw/0nTyKFjI60SVspRU/IFA6ZjhIz4ypUkdUvrSx93T2kE3FKpR3aro0Zly7LIR49f0FdkwhY2i0bKaFK2CY9+JlkUpV2N7a3+OjmXXYqDeYX1qk3O6oCuLG5qei4weEhEqk0k4eOqGeb0mC1o/Gn793i+9fmmd2tsbRV5Nb8ghqQUa11KFVbOL7JpWu3WNstUegd5MOPb3H5+l1u3p7llZ/+TBmcaqfF+3fucfmN16hubWBYlvUNUZX/+pe/yj//H/6AS+/8HNFE6nGT0DTZWNvk+KkTlHZ2mRg/wNLykppvKXFFrVZjcW5BTdY4cGCS8fFxypWqGp4lSYz0Tq9vrLK2vsGtmZs06g2kciDN/dJam0xZbGyuqYdvGBbHjj+gKhWNujSmSZ03gt3+6ydo/Fu/RC2qQm4enD6kJoXcvHmbarXNufvP0dfXh/SFT09Ps762ocYtnj53ltd/9honjh/nF55+mld++gpvvfMuTz37FCdOnqS3p08B6Nvf+haB4/HkE08yPjaiSPzxsSFMfDa313n0iccYPXCYza0yzWZNWaDxAwdwOx3Vjrzbcnjnw2tcv73A6naZiamjHD9+ClHiSFwpXaHdXT3k8xnWNjb2gBZTi3P6yEH6hvt5/OIjJHWd1ZUVwlhMnUOn1aJRK1Ov7qCFDtLXJE1rMm9UVYP0gPvOnuKFL77I6NQBxicmlBBHxDqOaBN0qYubxAxdVfHK5QrXb95iZnaerWqLRqOj4vOpiQPqHtWrFSXekNqatFMPDI0z2Bu1CP/s1iLfvjJHyUhTFfF326Memsyu71Cs22S7ulU588O7y7zx0S3KNZs3X3+Lq+99QGl9nfJuiaGRUYq7Na7fmWPt5lVaMp1E07VvnDlxkq+89JKyUjLxwUokqDaa/Om3voNpJhXH1pXN8OorP2JucZ6XX/4lWs0m3/3udxgaHmJ2bl5lgkIr3L51m63tbS48/AjT0wejPnFdp7xTp79/mBOnTnNg8oCyVqLy3i1vK6mUdCGms4O0GzKVQtyIhGGfgvOzf0fvRxz7J27cSvHFF7+gatJ3Z+fwZd5SIs7b77ytCGhR3gj7IDIzmeF59+5thocHVJ/O/NwiSRnScOoU7UaLG9dvqFLfgakpktkUDz/ysChbmL17j/vPnSSfS/PWWx8wO7tCo+Qo/akMdK3WGywvLDMxOk690aZcc/j46j12dluUKi1WN9fZ3tkml+nh8PRxqvWamrLR393F1nZR1bmFS23ZbTa31unNpqlsbZDvLhBPxOjOpqSfVeUCUkIUgEoHpKiT0pk0+UKeoYE+FTd35XIcO3RYTT9xXZvtrS3u3LlFJpNRnZTSeyTzp0RNJNn6/NI6RiyF13Fp1ircd/YkPV05CrkMA/293Lt3h3y+wKlzD5DKFvB8n+1mhzdvrjIrTX2eTU4GDAQmTizORqmKqxlk03GGunJ8NLfC8k6D+u4uuxurpJw2lmvT399DIpdnbW2HTsNm9dYVnGZFFpvxjUfOP0B/d56dcpWxySnefPMdRkcnuHHrDulsjla7ST6TUtWftY11RodHFbe1vb2lAnmJier1OqdPn8ETqkEy4USKnZ0dVS/NZnNUq01y2YLqS5mfn+P99z9Qq1D4OiHmZajB8NhhbNXYv6YIdUWefkaztw9IAalQW0K+i00VLZRUSX7v935fWeHZuVkefuQRjh47wqzKQgcVF/nx1auqbVhipaNHjlCrVvjxj37Mc889z6mTZ9R5r64ss7W1xW//1m8xMDzID195RdXbhT6SzFkmB7/77gdceu8y01NjfPGFJ2nVy2pYllSJRKy7eG9BAUCm4M3O3lNWSmIJES/bHhS3G7SaDn393YoykxE8y+trtOyWyoYLqTRD6RjHhoYpb26zsrmthifsbq2rNud6rSZsk0raIg0lUVdpR7J6h0ajSnc+y9riAquz9yhtb9FsdtTzmJ46QLVaUaMk6w2XW/fmWd3YUdUxie0axW1K29v09/VwcGqSZkMI+y5lgI4cO87kgYNKz1Bvtvh4eZsbS9vQaTKZjTFSyKoRljItUGrocp5jfVmyWsDlmXlcGTDblnYaA6dRU52d7UByiCapmCjJHBZmPsKXur0EV7bnMnn4IB9fv8vH3/0BRw8f5fXX3+HU8VMcPX2SmZkZNT2jWm6he/DzN95UZcgLj16g3Wpya2ZGafBmZ2fR9ZiaIDE62q/inFs3Z1RjW61WYXllgU6noizh1OiQajXdWK2qWrhMAY5n0ujV3J61VEUd5dKVTGNvWFTEtQpkIwlZSCSSzea7uXT5GguzM6ysrnJgsqjq1v29gzz11FOUdnYQediB8QmWV1ZUten27TsqE06l06ysbiBzi554+jHmZld47fXXabTqaG5ITyFPo1njjdd/ptKtl1/6AkMjI4wO9yNdnNLdWWu0WV5bYHxsQk3quHnzJvm+LiV7dtyOMu8CJtGVirKo6dbpVGJqSK2M8o7hKQt1dPwYB0fHMLQmN2fvku4fZGJ0Wo0j3C6usrWxFo0Lr0t8XiElfUcypCyTRjNN1Wlp+DajE+NqOnNle5tGq6PAJwMotzaLpLJJ3vvwCqubVTUSaHxsGAlRJg+Ms7ywxL27i8rwSOVL6LXbs/f48q98WSUoIrA+OjXM8vou//fb77G9vs3pw0cwGk1qOxUOjk8ot5yJZfDJMaCFXHrzHZobVfq6+lUitVPcVDOo+vv6sGQiswFeq0UiUcA0LES4p2LMeCzJ6TMPoMdTXPrwMulshntzs8oVSoVF4sPDhw4pHeTk5AH6+vrZ2tqgu7sLmf4gahUrEaNZb6o+H0kajh09zMjQkIptThw/RkqyQZnWe/a0GtK1sb5Gx44Gv4qbkXw7mRxUXQGV0pKawy7WcN9K7rv1qAVAPpCkSLVKqsTpiy99jfP3X2D+7l2VDXZ3DXDp3cvqQoVY39neYXJ8ksOHjpDJpBmfGOfWzG2efupZNZJ6fm6O8ZFhnrj4GJfefo+/+LM/49GHzyva6d6d24hKXGryR44d5Uu/9BJXrl3j/Q8+ZHJsmkqlzvr6KhMTk6pVQSgecfdSMZqdX1REdCh9PmrJSaHAx7PbqradNAKm+vKcmT7E/cfO4rQdrt+b493b86RHxuk/cJD+rkE1KiaWyWPFEmTSWUXHxKUen85EVopQcZcSrshzkeckxQnRpVZqDcUDF3oHKO42+PjGbbYrFUWxLS3OMTTQwwP3nVIDc2WBSkjWatuUy2W2t7exJWnUQ04cP4IlBLyhUchnOTc1wqPHDzCQTyJc6pV33iJRbzKiBySrJcLSJttLc6qSlUnGSbhNgnqF0HHpzliYgY0etJkYnWBnp8lmqUy7vE67VpZii/6N+86cJZlM88Zb7/D0c7+oBojK/PVzZ87x8zffUgnOmdNn0A1TZbG222J29i7dhQLrGxvK1TuilQzgwQcfUpMl4lZajZAubu8yMDCguibvzd5TguKF+XkW5hdUL4wM8Vpcki5CmZ+RUcOtWu0tNWtHymEChuhnL97cS8OjvChq2U0mc3zp5a9y7Nghbl1/T8VEQlKLIPehhx5S/TEyslqSscXFBTWUa211Ddv2+NKXfomtnS1Er7m8uIRUYYSo7u7pZnp6nEpZ/o8Pdnn22V9U7ck3Zm5Sq9fV0AcponZlC4he9N7cPJsbW1x8/HFKu0Vk9pHMqZ+5fVclUhLLuaFGxw1JBA6D4qpH+lQ1pL+7l/zoFPdqNW5XipBPcvbcOR69eJGuXB5dKl/iojsdNfxM1EPSXizdm1INE7bB83zV+y+JjerNarbZKu6SLkj9O6VmH80trFAsVdRU5fXNDVaW5unr7lKU1c2Z63x0+QrpdE4lZbVmR/Gbp86c49HHHpdqJPFEVo1OXFnZYmFlBbfVZrDQTV6GXzTrbJcqLK6sjbR/bgAAIABJREFUReelyzDahqraxfuHcJwmfmdXCbE9dHq78xw+OK7CsO1ikXKlTG9fgd31BRpVGdjm+QwN9zM5OcTN2TuK0JU5jYlkimq1xuD/Q9N7AEl6n+edv+7++uuce2Z6ctrd2ZwTIpHBBIgEKQaIpGWJd6VgpbN0pztflVl2+ersOl2Vyy6V5JNdlnikdZRl0RSTRAIgQIQFNmHTpJ2cuqdzjl93X73vQEuCKBAY7ITv+//f8Dy/Z2CQQ1PT7O0lWVxaZvbQFO12RU+r5cVFBodHOH7yGHfu3FII6vLSIoVSniMnPqUemHfeeYv7i3dVgCDrTTlVhwYTqsmTlIitXWFQfmSc+oi8JlsjFdrq0/cPymuHjnSkppLRiIhHRAAn9aV0nZlMiu99/2+Q6zkUDHPz9l0GhyfwBIKMTk4wOj6qlAwhonV7Ha7fvMnQ4Bivvf46yeweFy6cZ2VzncRQjE9+4he07o0lhnTk9HBjj9t3HuiqUByRAiCQk3VjdYn/9B/+H0aHx0inswyPjKgARJT1Umf3DDf1poUlV7nVJBr0MToUYTweISHmMpeXVDbPYiaHyxOjFhnkqTOniBpNLs6O0y53yaTydEzx+jTJ7m5iNz1qrRAAhCwo2u0eopc0PU5VsdetNj6fX/mjgl6Uofjm9rb6zmOROMVcitTeHrKIuHr+nAotpC/oWJYyBO4vzuP1h9jP57CZNoZnRnFHvCREOW/rk03m+Pk771MRLafpVYb9C5fP8OknRrHqFt/rXKNt77FvNejZLSxXGK/Ni8PWxHR5iIyOU9neZ2R6knwmS77aZzdfpd5p0sxm1Wh3oLo3DJYXFvn400/zz/7g9/nL7/w3fvbmz/mVX/3HpFJJKtUyjz3+KKn9NAtLa6osKpV6RGIx5VMKBLTdrlMoZFVYYbqcnDt7luXFJZxuJ48++SgBn1uLfVn8T02Oqbr33v17aoFIDI2wvvZQD8V2r6PSNqdwgvpNVa/IKOQAASPQCammxFBlY3xqHBlzVKoyR00QD3pxOv1kDx8iHIqRv/khLq+X6zeuHwgnPH4SwwlGp8a1lMhkizzz/PNsJ5PYvW4WFh4wMTbM3naWleWVAxwjJutbSVKZLN3+Av/kN35F67C3fvauKto31pb0Zbny6CNMpfap1Fp4PAGqZXF79rG3u8roHJwaYSoRJiJjGpcXCyebuSoN6rRsFn23jcOjflr1JmcScR4u3Oe/XL+maRTPPfq0+oYerq2TzSRVUY5NKCV+rSvLMloRXYHfRz6fxeN2cfz4CaLxOOvbuyzcW1B9o90wmZ9/gDCcTp+Y03QO+bhGQ8C84p0/IG90LCfpnT0OHztMu99jaXNbPenyMuXSu3y4sMX97T3yDbBkNRnyMzY8zOFEgmh8gLFYgLLdoukMkymUGR6awlbpkNlM0rH18Isvq92h0qjSEEUYdroS6CC61VCYrBxGomh3muY3BqIDVAs1cukc0+MTnDl2XGuLdL7AxMQUOzt7vPvue5w+c5LHH3+Uu3cesLuT0hqxUJQaU+JL0C9SWO3BUAgRTsi1J4CESr5ALpNHbKmlXI56va7WB4FGiaFqb3f7wG5ghrDZXLSbJXrduj6QIiYQAYO8AGJVkL8eGhjkj/7o/+Kf/v7v8eUvf5HpqTFKhaRuHDY3NhSUJRKqj33sY2qgEhWLDPxXV9d1Rri5uaWqbREIy3rv8KHDBASzXanw4P6i6kyD/iDf/Iv/V1+ux594UmlvXo+bQi7LWz97U7cTwUBEo2EGRsfJlMq898672CTRI53CIV9DvYkjNERgao7E+CxmKMxex2InW9aX8tSp00rX8BkwORDH1bFYfbCgzWUym2Pi8BzhyCD3F9bYz+bIpne1PpMRkRjwDjiZTRIjg+ztbetL/dhjj+mkREZm1Wodj8tDKrXH7u4moyMjHJ07TigU0VpYvnYx9om6S6RmpXKNvVRWu/cTx05wdPYY5UKdiD+C1+1le1fIKgvspHNalwfdLsaHY6ztbFNstogn4nqKz6+sYHN7ODo7RxgHH3/yEkMhJ5asUi0bbUT0EcDTt9PqWUwMxISAgcd0UEhuKXtVNz9Ol58HyxtkCnlOnTuDqEFe+9nPyGQLfOqTn6aQK3Dz5k1CQS/FQpZ0Ks/szGGK5TR7e7uMDE8yOzvD7m5SfSxnz55VIYdQMIRasbq8rPzxdHqP0eFRjp04paogGaX0em1y+Zxa38LhAV58/kkertxl7sgsX/2lL+pgWziUkuQgHiBRB/36r/0av/FPfkOvTmli5uamuHzpNFZXLLcrPJi/TyQSZnI8we1bNxifnGZ0VORhBnKdlYsVPY2bKvJdIZ1K6rDZ5fUxNzfH0FCU6+9fY3trm0+/9Cmmp6d1pShvutVsks9lOHJkTq/ra+99oKvQuakZ+pUyQaHNtVtkU3kW9grsf4R1TG+tUq1k1JV4eHqS4cEwieEgtWpeYbJbW9sqNLlx9w4Ts5NKihuKDVGo1tjezyiRo1bJ4RRvu8NU5I2IsgXnI9BdASCMT0zrS7y9vas3i7xEqytLalE5ceyYak6FGCLCYrFDiy272W7SaAmqpkY6m6PRrDA5OaK//5UL54hGpOYss5tL4woGkBtxdGxYewKjb9MSLVsuU6hVyeXTOnZaXFmnVWsxm5hUqWOpXmHm8DRzx0+xvp2n5bArNr9RapFrNOgLAK1VFzMwqa01mtUKhnRxHn+Az7/6i/i9Lv7r3/5QWTuHZmeYnpngv3z7z7XBefLJRwn6vLz+2k8RU7vUU7lcXk1PEimSye5Rr5f1C97a2tBrTUYLY5cv8PlXPs2Ln3iBP/nTf8/PfvYe5VpJT2G5mIcHB3G7TI6fPMGzz77A1PQMf/Wd/8jXv/6r/M7v/DZ3P3yXixevcuTocX74g+8jDdSJMyfoGXZylbLaOIRwLKf6ydMn+LePPsbuboZGs0k2s8e777/N4sI9rN5D/eGJNlOQ2ROzM2r1CIfdNGsVFheW8AcGuHD2JNevv8vJ00c4d/Yc7797nWdfDOI0bLRbdZKZjM5Go0MjTIwmGBsKEjUsarsrdJtp3l1cY2M7jcM9QMswmD5q4iqu4pEcpLFpnT/6bBZWu8va4rzK82T0FYnGOXr8GD2nk+1sioDfqeBcf8iDNeCj7bZxZOoCsWAYh9OvrlGxrqRSGc1MConhrNFgU7Zb9Nnf3qFWlhtvmIFEQu0UAmKQ01GaShFDy89eomiKpfJBoFilRjwa48KFK1y6eJH9TIbBRIJat8Vbb95SAESrWMLrCmLZA7REhiprYwv2d1NUK05l7tucPmr1Oh/ceF8htCvpffLlMqeOHqFvb2oXL2EQa5kSYZ+LiiwaDDtdp0H/Iz7pAe2NLvm9LebT+9pOPPux58lmdnn7rdd0PheND7KTSZG5s0u9UUeO+cz+LuV8Ub0cslacmBknGPSwl8xR78Cp8WnymT1GBmK88OJTuP0mTz5+hWvvvMvy/B1E/yyekd/+vd/lmWefJhKJap35J3/8xwzEhwkEItRqBT2Zf/9/flz/3ssvf5Km1aZUr5HMZek127htTlxOL9HBYfrOHvuFvOKm45Eos5MjPP7oI8wvrPHt7/wtdx+scePWbcqlAjaXXSV2wtc8cuSQDoR3tvP8+Ec/5viJGUZHp7l9e5nY4ISesNevfaAGsouXLnDx8jmctgaZjSU8Hgf1oMHC2hLLd+6SEyJyPMxUbIDHrl7AMFqUMxlmpqYpthqaNldv1kC4l7UaLqeDsfFxbWLmd1JkU1ncbgcRv5dStYBDqG42B5FoCF84SN/hICfii1KRUNBPPOpRMNfu1jZOt9xoRfaTKeTrP3nqNDJSkojAeq2lFD2vz0W9WdI6XepzEWbLmlhgvIdnDhOOxBlOTPP+rXV+8pPXOHvmGLFEFG9giD2pN3tuWvUe/lhIP/dcJa8WDUNO30KdTK5EXbS9ti6Vfoeo4cTZ77OzvkJmZ1P8MYxKRKFhYpgW6d09QVFTMiASi2MIbVnQjw6H4xuHJ6f45DNPMTk+qkS3gNvF6GCE2ZkJFW9MTc2o4nzxwX2sToeSCBeyu1h28R936Xc7uCwn1VyZtt3EIbJ6j5vPv/IpXnrpRQy3U0ca0o2fOnGM8fEx/IEgv/nbv8mnXvqUrgMb9QLZ9KZuC7726lf5hVdePoiua7UoZFJYQjgTjKDNrtF3Yl0VAYJkPQoIynT2SO4mWX64SV7i/6p1lW51amU8bjviRBR78bFT5/QqcxtObt+8zX7yQM41NTnNQCzKjeu3cXs87O4kuX79Bj2rTq1YUF/L577wOT722GVuv/0T7l+/Trth4Rs/xMOunU5oBEdonIFTZ3n6had59PgsZreNSxI+QmH9w22KzbejTHm5hmWFODAgeZUGuf19djY3ETOcy2ZXpVYyX9TbyeN160q02W6xvrWlWzaZIwqAYmd3n3yhoBOQjfVNJJxrdmaWkeFhFXuIK0D244mRBJcuX+H5F1/k8qWL+Lxe3nznXeqtlmoYjh8/yfPPPcXc0UkmDx3i9tI663tZtnZ2WFrdwsJDTbQ2rgATUpMHA6zvbKt/fjASxGpUdaQlKXmykzcNm65DJfgqU0xrz5LL59nY3SYtKqiupYQ9iS+UzCgRtIinv7C6RL2QPyAKS2sptYs3EORXXv0SH7z/DptbW5w4exa34y7JjRWuXH6EwU9/ktv377K0tkYmldHIO7/DBYEIfW+cX/zCl5mcEBLaCImBOJevnAWJNWl3DqBONoOJySmtMV9+xaEOyWo58xFht6903KtXzxHyhqgV9vUlkJFCrVIiFo2oRbhl1tTk5gpEVGmTK+3rSlBS1drVLuVKj/10CtPrYiIUIejo0OvV8Lud+E2LRjVNYjCMzwHPP3OBq1ev8s4711lemGdnZ5tPfeo5rjxylmw2zSdefIJWuUh2v8ALzz3GE888RjGX5Ooj53n6mae4t5nh7a0CZiBOr23HGIsTD/YZ8bnxt0tkEQ93V5mTbrPNxPg4YV9Iu2ApNUrlssK0hDXqDgZ45oXnVNku0wah6yXcLnVSyvC+5TK0+w6YLuUnpfMlyrUkrWpb57NSp8vqUJpOyS+SWlw2TsIsOnX6FJ/87C8wO3uUTqOj6qNiSdTnB0EIbtPDyMgYkfggvoBb18KicbWEzR8fQJA4++KArVV0Jr3dFiFIl5CE2A4E6MuyoNMlV69rfKPEJHrsDrwOKLdqihY3vFENvR0JeXVZIJMJsVTYnR6GEmFGo0EeuXiUP73/AbtLixgifRL2tzjZdjf3+EdffRWbYddtQS5TVlX3vTv32Fds3iQTY6OMxofxuJ3aIOWqfc4++RKf+cov8uVPPMmYKTDpg1/9fotOVwYCIshsaXMi5IxqMYug+8RkJp4Qsc4KNczR61EqF0hub2JK0oXpplIqIOLjSrvOQHwQe1PyLTsELKFdtCmWMzS6NhY3MixtJOk6XaxsreM2HBwajHJiahRbp8LYQIiThyfYy9X43Jc/yztv/JjE2BhPPfU4x07McPv2HR1pvfD8i/j9To3MExtpOZcmk8wwOjqKMIljgzG+/CtfwXD5sP/0XW40buExvfRsDQxbmUcjgww2q/SNniIGBdWoIV2qVbV0ayZ6g7zMCYWE0esRjQySLxc16i8cCKhdYtwU6VpevehylYtNNlcsasxNtZBUFVcpl9VIQTG4zUxPEI5FtYaUB1J+CVWl2eiQSudpdmw0OjLa6+jfEAaAnN6z07OcO3eeI8eP07U7uf9gg3u3HrCVrynBbzDop1XMEnBKwkaCeEyS4wSQ68Tugb4TmpYNVyBE1OnBJWEQ9bK++PIxtkqXRqeBz+PFZrppWjL2c+Dz+HH4IpqyPDUY5YWL0zx24Qzf+rd/rAIRQ/DICw/nefrJJ5n1HOXB8jqpTEa90strSZ568lGeePSKokumBoY4OTbGnYUNzj3/DCde+QKv31jk0umzfPaJRxiR4lUCOW2CJ5AZeVcJGo6eAPZbVMo58tmCKlD8EjpqtShmszidLjLJfQVjiYpbchMDwRiJoQR2R4+ljW1VCx0/LGJgeWmytKyH0HVo+Gmp7+GbP3yPO5s7uH0G9k6HC4emaQWayAbDZ5pks3nOnDrOc4kJwvE4k1/+Im3LrvZb4fE899zHMOxu9RRJoKoU9dl0SZMinC47K8v3yReqHDl7hl6nRreyzVAwwOFQkKWdDJbfziEnxDp1BCHUMr24DTden0EpX9DxkswZRYTrchqMjya0203EEpTKFQYGQ0TjUVUwiVrfdBsMuwY0QvDDO/e5c3eeWqtJpdmiIFd8oYyMa8YGB/AGgxhutzaeclLKL3ngheckLtTudhLDHVDogdBr61ZDT8YrVy5z/NgJJmZmsLlcyCcuFoz5xQUcngADgzHy6W18hkk4FlHvkNTEjr5Tcy9xC41ZVnFuOk0HZt/QaUjZYaNTKzA9OclTl87TbJQp19v819feoiQRht06FWlEvEM4BaVeaFIoWHx4c0cV88I+MoQYPBxPcP7oKf70z/4z++UKn/3MZ/nyP5ojmcpz7MojBO11xidmKLW7OOWH8eJzNA7N4ejY+fojj/LEYJABU5AnnQN4p/BvJOpE3lpNWWipJOz9d2+wuLiMwxPDFwridfawqlX8fo8y0sXnk0zmVW0eCVfIFsqK+Ls1/5DhxCRda4XhWIBMqcBepqAsc8EU4o9QrpSoF+SPFvGAl56kY2Qsql47rsEwDVuTvf1tnSxkRFUvhhRM1YUKyKFt9VVwaxrCeJfrt8Pi0kPuz68yOhhXHOI3v/1tFR5funxJgwge7qbJ5tKY/TZnAnGmQ4JMLNHoSgJwUK0aMuQXzruAWX1uUyltlVKJ939+S39w3XoTu9fHx595AadpKhbmwZ07pPIFdjN5dvazWgfKi14vlyjlRRnkUvme8IQkkFYiAYXp5BQvlFxOYnQS5pRlMTCc4KXPvULbamj/YLMcWK0q0Yif559/lkypwp2VZcqNFq2Ohd1wMnniJFZDpBR9ZRYNxA+gYALyEmiBWHdxdDTj3i5Zlw75eRsYbkPV+qKdmJk5zLETc0yMjTA+eJL5jSSHljfYyWU1dU+SSrJNmzbQEuj6s0qVQwk36UxS//0O02V+w+sM4eg5uXDpNL6gYCS6PHP1CWzDk+wMjeGMjJEYPUQ9GMAXT3Do2FHCYS8Dnj6TASdxr4kg6iT+XWJNRMUiMcUy92vW6rpHFVCB8CN397O8P7/Keiqr2DoJm5cMm83tJNeu3yGZzioeJV8oUq002N/LkE7n1ABXr1bIloqqks5U6/oDD0ciZMsV3vj523SbDcxeF7vV1pz0vtWmXZcm6KNNjPzYeh3KjSpb+2mFnErmdzGXJ53Nqgd7dWVV16+ibv/g7gLvfbiA4fIwkBjlzXevcf3WLZo9C8vwkSqUCUd8nB4NMe0W0ECJWruK7LL9bjGHHeRyyrBfIKn1ek1V+6IriMej+pJU6hVe+vzncbtD2kyNjw7q1/gf/vN3tMOt1uWBypLe29PYQwE2TExMEgyFlb8uA2rdw1uWorMFyyi4GmGvl+tNRidnefmVz4IomAwB4Cpjh2K5xgMZ3OfK9AwXnmBY5XB7OxtYRh9PyKcne7/TY3x4CK+7h9fj0IG9eKWEgizbLXFgCpiiXiyS288oB0kaGdkmLa6uS3ge5XaPdKVHz/DpPNmJQTmfx+PsEnLVidgqkNwks3aflfU1apJeZ5rOb4gtd2x6iiNzh0iMJnD37Dz4cInyyCjuETnmQzSNLk+fmuTK9CAJD8QleMnjJmCzlFMu6V9CMJPxhMSfSCeYzeyTzaTJZAWCKkHvdv7mb/+Od248wOMP4xBxQqNBs9nl/Q9u0rSEh2lnaWmFzY0dFSYk9zOI9k+2RZls9iB7xzApV2qqGRTMijy4kjku+ECXcG8keMAtkABoSoiBRP0ZBhIaoCkQZpAbHy7z59/6aza2MzQbkvkDhWpTMTE///l73Lm/xOLKFh/en2d1eYW93R3eu3ZdzCjEIkMadHBkKMrZ0Qhmp04dk7bDwC9GN9dBDJ909xIMJSkTQvy1ybXntOvWR2gnssI8c/kRxee88drPiMXiWt9LIyT7asHFbGxs4HV5VBkl05FgKKK+d5HwaQb5R9HToh0Qf480VTI5ESGvNDCnzp1VZddgSK5mqWXrsu/TNeuNW3dYWlunWGvijkRpdnoqkJYTWbSjMoQPBoL685URl9yBGnHYd6gwRHb00vSI9VvqRrGNSMyjiGmbnTbuUIy1TIX5rTR3NwvcnN9k4+EGpVaTUs8iYG8zUC5i7O1RSW9TqmTZLRapt9oYcnxfuXCc4bCTmzfucfzKJUbOjXNxaJDg8BCyDdmq1glJOq6tq188VkehB8VWTu4N3TzUZJsgY4LxMYXnC5NybXVLvdDyezTbPd59912++4MfYQQGmJHYZJ9JvdFXKdXs3BHevnaNUqmufCHhegtyROR0G5vb6hUXWL/M4+aOztIoFqiXwqTqDV2lirg21T04BaWhawvHvWPX8cnW9g65yoxaUb0OB9HQGq6Aj6WVNWqdvqppjh4/oZ+/JLZ1bSZ/873vqodawPxWrcSNt9/U4f/4QJiIYRGz1/D1vWxsFfWkikfCFDNVOoZBNB7QU0fIGx6Pi26rST6zS1LWsR20CZGHwGa4ic/1VSP62MdGCYS95IUW5w7xieefoJBN88ab7xCNhDGdHg02Fdu0rGY7vR69Vkd57Bo0Kxshm52jJ46rx2kqMYqQRl767MsKqjo0OY7T5+XW3WWW17fwBtzExhKkqiW9xtMFwdu0cPVMzF4L02Hn8KkT+PweUmtbNGsGzVqffrHEyIjI8IQB0D/4nNoN8rkSGG5MT18TPCSfScQifYeHhsB1nT6CwRiGq8tAzE8nY8fYWqZSz5KUuWynrpoFyWqSX4qIKecynHnxJTZqBoHEEBcvHWUiGsHWkWuwzpALjJ4No91DXHotCbjv2CiV65Qyad2BigvRHwqyXCmTyma4efs+yWRWZVL72Qx35u+oncJpBpVLJIApl61PRCwBQYNIcIBGsUm9VFEdaLVaIxDw4PNE6dRrFOWH4HKxtbtDKr1LJOAjER9go7CrzZIotx1OqXN7dG0N9vd3aDYChP0BNjZ2dM8reGgZPLudfZX0F3NlcrkPtfmSlI2b19/n6edf1Eag1WlSKubweTxExoc5PDPFkUMzxKNhJV74A17sHpOOjEjkwUtu02tJM2DSaYthTOCxFrWmne1Mjvdu3lVOuTz0nkCYniAenS1yhSzTUxM4vUGFi8kLLA1fMrXDY5dOUyvmWdtNUa7XdJQkteaBeklS3VoKa3UaTo2nEb/3+JGjHD51jkOTUwwPxwlHAri9Qao9O85qi+mxAe4vfEir69aTVJpPYaDWCy5NNtabr9/BFR7A6fUgWPXR6XHKmbLeWD2Pi5rMKJ12RKFakvWhLAAGh2gKsrLVoy30jlaToM9FwOUjVU5TsUp0610a1RIBy4Ot1WAnt6eOz7ZEKJs25YvKraoPppwuHcPN5LlzuEp1Th6fIeH1ICAnKXRl8tDsSvpYh1g4iL1TpdtpKaemL+IKHBoxJ068fK3JX33v+6xu7lCttQkFQmQzsq9d1jApsfdKsq4oPorFgr6VwjNP3U1TKgkuT66LvtZiglpKp1KK4pMGSmzCsq2S0IJCroqtO0S5bmF3m/hDfpa3t9RuarOksbGpn0WvtGZH2fAd4bY7euzv7+LzulhdXdOT/ld+9Zcplsu89qMfkdzZIpXa14G/nAhzM1NMjgwxOBBlfGyYkeEhwqGQqoBEJypBANV0UgEMslKTHEcZg0niRDZbZOHBKlvbu+xn0vj8fmKDB7jBakOCBCwNGqgUC4rJCYZDB7VjMErXajE6PoMHGxfOXeIHf/9T/uOff1Nx2/JDk1WiIdjrTkex1wratdkQIILPH8CJG8MT4YOFVcKZIq2OSa5QYSjq4rknLvF7v/nrqlQXbWrI3mY/l+fW/DzRSAKPGcDpc1Dudbn2wVuMRvwcnz1Cz9kkOhEhX6yojVnQhX2ziyVpwQ43bYcM03qasy7Lj3BEOvodZo/OUkv56ae2ibdzxKlSXN5kc3+TfLOG3ePC4zIxZZHatrSR0wdTdH1HDh/j+NE5pptV3B4BxnfVkdfvG9TKNVp9g1AsTEd3vG2lTuztZonHBvEFQ2wlU3x4/QZ3F1d57+adA+ZipUrAm6WYy+qb7XI41XEowaVCdpBGoBX0UW05WdtYI5fN6XxNr4i29REt+MA+IVeX1ZP88S4uj19DSk23X4315UaOC2dOc/P+lipbhCpsNyT726Um/pq9oZDQfkdmBHLKNClk9jWv54/+zb/il7/2JX7/D/6Q5M4KYojr1St4fU5mjs4wNjTE7PiEClgNUyRiTRXHFtJZnFJHVkqExdIgiWSRuIYaSD39xlvvsLmxqcJpCUkNRYKamVSti9enpjiZxMg4ZrujGO6//eEP+KWvfY3T5y6qUl6SNySNV7Zn0iULs1Lmv7VGVQUf8vI2rS5Ny8Lt93Hy+ElSqTTnL50nHh+gXOyQrlq8e3+dnrmL1xNjfzvJeMLFqROHCLp8RLw+EmdP8diFU2o8/PHrb2lWUcTrIlep8rdvvcNoZJChgI/8TlKv/c39LG6bidPwUOs0sFmWuI11mJ/OCxH6gLfucdipFSS0tswHt24Ss2C0Xsas59nI73Bvc5tsMaNTkKHEkN4szUqNWHRIhTHyk9JduWEKZ93CKzk1Vo++hMyLy9DqE/X2yTfrZNNNUo02/VZVdX7bqRLtCSfjYxFmj8zyZ9/+/3jjpz8nGBrQGVejlKOWk09UiJVObMLfEb67+KA9HjqdjjZG3XZLvdByHYjCXJohSSGTE0kkbjJz0kwlq6Me6X+FfCznAAAgAElEQVQwqMkutttrkUuV6J8wiIQ9VHf26ckVajOxuWzYOi36DqG3Cf7GVFC90yWbBg//5l//C772tS+R3Fxmcf6+iotFAT8lJ2Q8oqtCvz/EcEK87kWaNVkU9EnvJvUFCkRCmqohVA1Jyc3na6zfW1RfebVUIz4QJxTw0WwIQLVItVHH4/UzMTHLqVOnkO5/ZHSE7//dTxidnGZs6hBCgHN4HGw/3OPBwgLNQpaZkQTtSoN+105dbhssHbccKOL7zIxPcfrsRQb30zz66JMMDo+yspHmb/7+DU1OtpkWsZ7EwnQI9u0Ij2NpZVMxPf1eXdGCF8+e5Quf+zztboud9UUOGRNa3sh+f2p8iB/+8Me88NyTrG1s887t+2znK0RCPoyeC8dHqOyQU1KW29g0tbjKvft3kdXRkZFRPPU8rWKe9XKJ+3tbZCol6QHVWZBPFxCp5EBiiImZI+yXSuRkJSnHZtuSaqEtydoYQlOT5qZSoZxOYuvV9GjvNXq8fWOVvVxFNZXpXE6v7GevXuDY0Wm+/uoXWXkwTy5dwiZJtVZT2e7Cc5HuTp4uyTKXEY6MM8QHXWm1aTUFASO5lFVdVbWogyCrPwLcy+lg14gXpybWim5QssUnp0YZHR1mZWmTv/7r7+tpbpiSggZOwWBL0KnTTl+2K82W8Ihxuw2FTP2vv/9bPPr4FarFPW28vvZLv8h7793i6NE54pGIpkGI4km8Qg7zII7PCAdxu9w0YjVcppOm+OZLZXa29liYX2Q/mUHcovGBQQWNSZeaz5f1VBVYwcRgAskRnztyTKcfkgAibsUv/OKXWFnfoVVp4jUkdaKtYVkfvPc+J+eO0OwZFGpNdjI5CS9WU5u8XDLCGh0Z5dLjT+KLhDg+EFOAqij69xslGobMF0Nq5S3kNnjiwlGeeuS8Pvw/ees6yayIRVqqYio1m5w5fopitsD/9s/+b46cPMQ//qVXGZUBe6PKpaef1VCGi2fPMBCP8t0f/T3JUk1HQYZsgBwg2J2g30alkFW1VtxhMWIauDKrpOtdCHkVO+jPVeg1e9og10o1HaP5/CGOzp1mYGAUu/223nyS5/aNq5evKnhV6GgSiafzxr1t3rtxh0bbofk3nkCAYsvirfdvUau3mV/f5MP791Vku72xpTk1csrdvHuXnlzbGhLVw6GWnYM4DUG+SPyzvO2G3dA/i86yXpVatqnKEhGFdLvy5tl1BCECYZVqOQyFfspDKsg9p81gemJaNXzrO7tYuHCYPhWbUK/TKuXVoyRUDBmrCEl4YnSQP/l3/5rzFy/SaVT11JZi+9TJ4xw9Mot4sdstoaWJsEGSMA5ywIU/Lqen/NkXiuiQ+P1bt3nvg+t6QtbrDdUauD1uveKLlRK1Rk1niQJQeO6F57l06TKC1zZdfWLxMOMTY3zrW98mGAqym9zRk/Dc2ZOKvnabTh2WB31+lpaWyebz7KZSajvwhwKMTU6pTUFiV8YmJhgIydYoQtPW5/7KJu8/eKgStfFIXNDGhHxuoj6D/bUtUrtJUsUaq7t7OOxtrl4+qyvVXLLID3/wOt994z3s8TjVrp2NQo2dZh/L8HPt1gIrm2mchlcPhmK5Qr5c1fDbXL9DySmQWojUO/ibNfx9IX6InM2BP3GYngnDwwZXLlxgeHhWox0F9jA2PsH58xeJxgZVM7G28VBvGA0HkHxB2anKMssISbaPhSUUHKPLw620JMbRM7JMDka4dGxc4fhbm5t0bU7+4rs/IrWyyFc+91kevfQ43/6rv9HYD5uGDklU84FCWjjpQnKQjD0ZNpviY9HZpk23F5KrKCFWGlFtExFC5yB7RjY7ckp20bQxMbxJ6Gkuk2M/mcZjSpCpRd/jgq6HfruJMJa8QbdeLXZvQE+USifF0089wdCQ5Hk36dud2hlXGzWcdsdB+HytwVsP7nP4yAkm5iQxQoS5Aom1KSntwb15FpaXWN/eotPv64bC5w0qiYT2gRwvW8grvHRiakoV44JskZXn9tYOXp9bCczysMn7Kqu3hcUFvvTlr6h3ai+b1fJG9AEzhw7xrT//Jg/u3VWFkYSXCqzg3NnzHD1+UkMNpmYPK+Pd3upQa9m4V9jn5to2tS4civmZ9HRppjKcOXIMZ6eu5JTNXIFmz0lxZ4eh2BSnjh+jkq2Q2iuQKuR19ShQr/m9NMvlJlMzBmXLxPLGdLZ8e34LZ09EvXackRCNch1Pv081vUZXVtB1UcHvqmUiMT6H2++m2khz5USQT7xwhjvX89TrB/6kkD+qs1a5SaWHsAlmUs1eklfe72O6XBrGKam2gi9u1Sp4TQcD4QD3drcYjwyrTF+wxkN+L0ZPaA0lXP4we7t75EsV/vjP/hPjo8M0hHfT7SoxQrflsiMzxPts6HpSGhkZfEuDJThB2enKH+odl8B3+Ujx9ujz2MPhcB8AtqTn64tdSOqsHi2rxcraqkqnfN4ILaeLVtNSGZzhjqmYoJkvIbzzEF1efeVT/J//6p/jMu2KCdSYmL6hZDeNZOl3GJkax/S62UluM314imhUtiFV5pcW+fDDuwpCEJ+MBNxLapg0NmJzrTQbatWNJ4Z44uIFfaiSyRQ+r4fZmUNIlrjYOU6dPkOp2OSvvvPf1bJy9vQVNrd3sds8pHNV7OU29UqbZkNqc8EDdoiEosh3MxAOcP7iOY6fOEmt0dLTRVx5Io2TB7zYqLNaqGBEIvStrOZxSuTK4fgAtlwOy4BCr8d+pUpjL0+k1cWLk7c+uMehmWOYwT4vv/wCn335E2zms7w+f49obEJ7jpv35um1bXSrDZrZfbLrKwxPDNN1g5HLc8hhQiVHqZrkXrlA0+1jaGhK3bNmIMeXXj3MmVMRLQ9z2bLK3CSUVT5/WXzIi6/oQ7ktLUm9sx3UmPKkiG9bfkCdtnB38nTbFj6Hj43NdR4szHN46ijjibiyjIRQJvvj/f2cahXtlkDmuyw/fKiZ4hJsJLq8voSR6slpam10kIx1UCNakpQh/9E4DfGcHOx4XbLi6jpoVa2Pmp8Dr0+n1dMHXtO/RCzS65LMJImERzAdImLwgr2hSh7THabYqOELhLh0dIZnr17k85/7jNaGspcVWJWMj0zTq0RikXDVakWEMeePBllaWObGrfdJ7WfJ5CrcvXdP7c2iYTwI5pL4GUt9OBJTGBuI89gzTxEM+HUCcfb0Gb2yBGwlmgoZkx07cQwhkMj35pFHruiJJzElfrUr2DXOpFiRNIoOA4NxnRKMj4+oNz8cGyA2EGN4NKFD+fXdpI6muk2o2g3McJD9bIGa7MElGkVOxFaXt1K7uNwOgkafRDxMp+UhKEYxu0FobASrYfDmOw/56bVtxqMBPnb5tOIZ+6l97PKAdJvKaWrXaqwubdIoVQggnXiX5NoDPJUiM14XRXuL3XqOWs/B6MBh3JJi3Mly6YkZPvWJ48TDDn2m+gQpVsrkS4LzdiquUrb7UtYJ/HXxwbyODQWTo82PDhblcpEZZUMyZZLsbO9okOnyygpv/PgNXn7lixTHR5TwJlS0eqmAQ4LmkYGwDRcCU5WYYUsfNlG2yGpKajjxOoslWPKEnH1xPaKrNzmhJQ5Ea055e1xeDI8Xw+5TQYOIFuQNUvplr6PjJmcoQrvZ1AbL63VTrORwR+IKhzI9YSpWg7Bp8MKFczx7/jgTwzHiwwkGRuLKl5SU2GqrSbXZoVUp68qw163q9eP3mjz97JNsrm/x37/3Ez7xC5/BF+0QGRjkzq1bSmOTU1mQOWKnDUdjDA+PcfHyZdw+DzOTU9y8fl0TJPqdJpJZLopzSQOW09N02Njc3Obc5YvqswkEQ4x6fQrVigSCDAveu9dje38Hl8fBUx9/UoFjUm/L5uf1d67RsrlwB7z4R2RTd5s7m9uMnz5B1BfTa7XusOGWFLKuRbXfIeIKqhzuYWofq9ki2K3iCHnZo8t0MKyx3jv1PGXbELn3F9jf3WZuKMREKIqjUye7vUolU8DWtTSa2ypW6GS38VS3mJoYptXJsVMp4osOcSgxSTWXZXLYwee+cIZz54awKjX2N5v0XahGIZ2VkZeElKKeI6/NQTGXZn75vhr/JBlP7B76YNrkte7VKOb2EbJXOV+mWqxphN0nX3yBUrGu2S43DCejE1Pcv39PPSMuAVWJvEpSXA8G9lo7CentoGE56MSlPpBrT0OmDDsuifS127HLqSUKdMlAdLRVumWzOdX30XP26NjKavUNuNwKlvIEo9R60LK6yApUBLpyNQ8KnU2K/HCQlx8/w5Vjk0zGPZRz+zSaRaYPPYJhGpptU2s2SBerJDMlRMUus7hKKa3iY4f4eoQL/3BD60+7qIKaFW1i2m1piGpq9gqEAgwOTWl9JxhsebkSg4PKnI9EIzSbdWX+SG7P5atXkXgR4RPJwyuwBNkti0O0Ic7CoSGyhQIrq+v43OIZb+LyGszMTivgdHV1i2q+xs07d1lPlQnEY2qXXlpfotWVyUeD/fUFynZTV6MOX0hTLTr1FsMDY5rUUSqXcLSK9Fot0s4o4biHaRrU9pNgOXD3DfxOH4XtDRz1DLvtIuOTo8wlJrh+/aZ+T6rtGsN+P0GrR2uvwMjAMJVGmwY9jp+8QMAXp94ocOmpSV765ByGI082tY/bDFPt9DWWZS9lo1YzsDskt0keARsbm2uKDgqEfQpskIRmqb/1wRRzVr9RI7uf1CgPSUmLDQ5zZ/7BgUzNNMhXSjjsJtm795U7I49ZTwbxkqQmIVByfeveRrjo8t+DxFU5HbWOlaAkiQL8aGzU1Zg5E5/gmjuiXg/oOMbrPSDKNtINrUFCwQBT46NKnJMXIODzE/EHddhdrMoKs8p4IsITVy/x+IWjTEQkxLSr67EjV55kfHrmIBy11cASi2q1wXYyQzpbJhoMaACBHOGq0s4U2V5bEMmiqunfeOOnDA0O6BxPhA3nz53n6NGTHDl6SCV+MuLK58oaG/LWGz9jcmpSSXc+n6xZg6qSWVlaVuBqfHhABTJTs9MIb3JkfFwFI+lMmnylSr3aJiZsS5+JRKn4PCFtDj0+H4bdRfX+Ih2HQSpfopOrqXvRsHmYHD2sWeH1ShlPx8KWrSDhpSKhq1WL6kL0OV1EJQvRalLvWnjEVenrIlljNG3ExPKR28HbqhEQdVnfQa2Q593XtthcXcVye5mUwyG/Q7yape81aDj6+EJDjI1IKeWgUd3hM6/McfJYDKuVpFK2cDj81Ft9clUXpaaTG7czNC1JBrFjtVusrT8kl00RDPmQiYbU1FLa6eZH/kcfHmwqSpXgz929NAPD44QHRnn9jT9jfXUDMzyAaO+sRkOJwTKCsUleoTQzAu7X/MEDDaZIrmQYLcNIceTZ2l2a3Zpe+Q6ngV04j722ahobPRtO8WfbpeYw6LtduBwOWuuLDAZDjI/F2UnvE42OQKujnbjP5cRl9BmN+3Alhrh0aoaLx8c0O/z2fBLLiPLIUy8wc+yQRjhbrQ6NZpWuTfK/c2xu7mmuofw+AmMQdJ7H9JHe2uL6teuqMxQNZTqdIpXa5bnnn9Xm8PDhIzSaEsksDPqqrv/mjhwnk84SCgSp1eoaPCC2YNEsjo9NEPB4cFltFdBKoyQbI/FvDw4mkEyfrb0dotEYsQG38t1llyx1+cOlLWHZEh0MY7UrRCMBbs6v0HOLEtzOTrKCzx3QgXaz1iIai2DZvZo7KSVCq9tSIOyhwQF2N3dpOxx4PQHGfS4dWbX6fcSeIqLostXC5+zi84eVLpcIekhti74gQ3Y7ydxonEfmptnY3aTcbWDEAriDMXyBOIbNpfPqoSEPJ+cGSW+ltTEUt6M3aKdY6LOzZ+fazQ0KeQfegKnJaRsrSzRbFTwBJx75nJwevWn04TxofqQBkZ2zQTAQUnzy93/4QxZW9glGBmg0+oolkZ22SMwq7ZqSaHXXriGZsovpY9iku5JrvaMrR8lJFIqX9NkyNBaNprTaVkfiUZx4Q356fRPDE8bp8tIVZXYxR6/fxmVvkRj0MxwOK8emJ+YTuwyVXfS6aZ2Rnjt3hscfv0ilUtCr8tpbbxIaSuAdHmdgeJKmeJel0ZF9smQmNpsavxzwugi65KsxGRkaolzOawqH6ajJKgKr1VW1Ut9lcOz0CU6fOEEqleLkqZNsbmwjkALDaadaK/Fg4b4ywwMhD5FoEKfpJRSKcev2dZaWHjIzO8vEoVlVr0vks8SkTE1Oaa5QNp0iNjBA2B/SaOdcucTiw2VGY3GalSoZ4R/ZLEIZv/rCXY4uzzx+ibfev43R9dPq20jt7SLuRK9b3AA2bGJ8m5hW+0J+bwV3JY+/06aVyrNabzE1O0kk3Kdh6xLyhZW3v1Wo0nN6ODQepbO3hs1hsZfdU9Of125nQmD+RouN1fs0HWAOTmqqmYzHpBGUiYA8TNJoFkoOqlUfk9MhLFuT3d0ON28XuLu8T6fnx/SYbO+ssC1BZNiRhBNpGKXMKeazTE1OIA2gpLPpVS5XsMjX6o22dnuyMlxcWaHbWdEHVrB5miauQ2+pKyUsXRY0si+U4bkkq4ryW8Y8Muf5SL0ut7pI8V0GXcnL7suQXEjFsvu2sDtM5VwK+L5aKur6kkaJoM+uoyeRzYk6u1ytkE5fZ2Z6kuefusozT1xhampcU9I69ao+mHfmH5KqtDh6dEBztEu5NB+225poJnebQ5UvTbW9+kVJ7vTQkMB7j1OZRA9XVnj37bdIra8SGYjiEkS13al0uGAwgGAF260ud+58eEDhLRe58+EdFueXePXLX6RcLhCLmeRzaRqNOocOHWYwMcLO7p6OrPJpMc1VdKDu8zh13+8x7XQVYVijWCiTy5cp1psEPCajsTC7ezvqJhQFkqj8w0MhwoMBnDa/ggQi9j7xsCSMCVirTGh4UB2J3k6HK2MJTUAWSZktHqLXNNnumGzuVgnF/OQ6FQa6kuHTICj0uF5PP+9Q1MfWwxLDXhfHoi46zhKVTpum/SAqULY0NquLw3nghpTbUqjLNA0a5SKRwSaNvpPl5TYfvJ9hc7eM4Q/R73RYWLyljbVs1aTJkXJHckmTqSznz13id3/rd/jDf/6/c/vevY+aHxkaSlC8zUlkYIhILIxT4jWEJSRHY9/Aali0GmW9bqXPkY5aTkFFzSj36uAhlS5cNkCip5TtT9vWw2HaNCfI0XXK4JReva2JsKZX9uFiRuvT60iJ0GMw6GUiHtSQqr29DJF4jFjYx/G5wzz99OPaHR6eHNPgznyxiFuGsn07R46f5GQ0piFW9k6du++8SSgxyfSx4+RLaWjbCft8OPs2xMQlO3Rhx/eEo5PPsb2xoeojyXSU/0/mlVub2/zFN7/Fpz/9oq4rr39wi/39hp6gc8ePcf7CJVaXHmLYTVUGyTdD2JzCR5dwU1FuSRxfLBzWGJGdnS3200kOHznKQHxAy4FQ0MPdhU3qFpq9eGf1Id66QylzskiIOCNYNheVdp8HN+7R6h3wML3ye87OcOTcEd27V/JFylurGI0u/kiMwPA0W6l9VpbzuHx29YHbujJNttEqlSUXBEfFhs9r4Oq3WNnYx+xA0Ooz6+njbaQ0aaMmgmGHjdBgAqcroDNmu4g1xKjQk2xPG+JQjQRlumBQqvv44E6Dazd2VYPrCkSp1EosLN6h1Sio4j3gC+PyyMq3qdusz7zyBT7/+a8qukapIqpZs9m/8cjlCzwp3WOxqsEAck2eO3uGldWHZFI5JKZNiLjqKJEbWU5ESSYTTbPIS6QB0ofzwICmwVAai2zHIW5ITcuVduggZloG6HLJy2hEPkL22iIiGYh6dHi9urmprsGRoYTG1b3wxGU+88kXGRtNKM9dlE1+t0fjVWymE5vLo9xIQSjfu/0Bf/+T19ndy3D1yiN63aTS+5QLFcK+gJYX8rZ7fSH1j+cLOVXAm3Y7yY01+tIkCK1YJH09mxLvRH0+PT2pJ5iwKa22fuU8/fQzDMbiWhuKglzWkJJXLl5vwVj7pAsv5PF6fARCEY0iEYGwJAAXClWSqSR+l5OA18NOKUtgIEa3Y7E8v8jy6ip7+xmNlQlGBQcdZjedw9E3aOXKdJoVpk8fItsscfTwNMemRpl/5+c4ak32Umk+vP+AdL6CzzeA3xtRbGHIDYMRF6ZdxNmmnDeY/gCievLTItHv4tzdw6hmNUZwr9agYfgVFCY/Y6cI8E1DDyO5imXmI4uGSjXP1JEAdp+Xn7yR5/aDfUUuOg1TG+qVh/dot0oEgn6lSpsOQ2OuRUPwP/za7/Hyy6/qwWgYLr73/f/G2tqKHIj2b5w/fZTDU+Ps7GYUOS3FuaRHHDl0iOTujkbxyehEBBSCvuvLTJGuduIiVhB1gUKn5enU+VRP55Y2p3zxBqbDVEmVjjYl2N10YnhNep2WfrGytoxFQ6rJy6QzuLwmL338Wb7wmU8zMRLXoa86KcUv7nQoa0i4jqK52spkmV/Z5Oatu9y8dYuF5WVqtTbh4TFio1MqHKjl8ypmtRsHKy95HertjkrLRAMqYxunQ2q2LeWai3P0IHTJolqrKxnNcJoaxSJKoguXLyuMS8xgot8UCZ/McgXgL7gTQYDLTfLsc88hnPlup6fJFTKTdXvdbGwmWVh+qJ+bx+U4EIVYfd659r4CYOUAkG2aWEFEjF2rdUhlJArRTk9CqlpVvCEXUpdKeeGmzfHDk5w5ewZ/JCywCxJ+D27JBVIT3h4i0Pb5nbp4aDuD1F1enBGPhim4q0VGS3n8Wxu0q3m2pMa17HQdhmpGZUohjHXR57pcLlxOH4aM3uX677Spdxp4/QFu3dtmbauqX6PoGdYerrKxvUS7UycaDpCIRHHIeK5cZGxsgt/63f+FS+efVGuLXMwyzfjud7+jD6Yq2Hv2PoubKyws7DF37KzKyX7wo59y/cZNHfDKd9myeqrykQG6XOPyL5L1pZx+Pbuh15+MhaTmFEuBTKLsjoOuXRohORzFAyPNeq/XoVWvHTRGPYvhaFwj4eQUferxKzz99KMcGktIOBBTYzEqNcmysfDbJNavTy6d4qdvvE7X4SKVK+lJZLpE1gYBb4hIfJjzV54gEI2wvrHO/M2bTM0cpmy1kdlrpyW+FMErS1iog8z+HjarrXNbET8Lmq9Q2idbKDI9c4QzZ8/rC3n+3AWVo8k1JOQ7keW5vC6tzRyNA4GzmMz8waPKnBe34ukz53n7zTeRsmNqalLB/3fuv6luRtnxSyipfH/u3Fng/v15IuMTjM7OcDQaJ53MaLnkkLCtQlWRkB7TwOEzqbUPxjzeRhuj3mZteQu7K0YvMEZozCCV2tKbzdNuMhHp0zPz9JuSd+umardo253080USlRyD1TRGM0+20WBZFFHtJnbDRTQY0eWIzHclDqbT6mB3BTBN4RZ1qLVb2tNi9/JgPkffJh4hv4IcVpeXqFTyWH1J0BvQ8IJCNo/b4eDKI4/y6lf/RyLxcUWmiwJfDoO+BInJiEieHnmz2+Jkk01It8XDlUXS6STra9usrezqgyepZfJL4uVkMC6iMtVKyoPoEGFxH7shWx6pJe04XZJzbalqpdNu0e2Jg9BOIBan00dhT+LYM02DkNdD2N5lcmaMkalRJmcmGZWggtSuijsM09SrTgLfRTxxf2GBzdVtHRuZHi+mx4fhcqgaXhRKdtONER8h3XXS2k9T2d08EPh2ORj0yh6/B4IU9IW9xAcjOA343l/+Je2WpbWvDL9FmtdsyvC9qtI2n18Ezn3OnjmpkXKiuDcMJzHJIS/kqZYKqgUIhqJqmMuVVlhdX1WeZTgaJl/Iq59pfmFV+ULtXpvlxRVsfSehsI9Gq6w+HAMnO6s72BxtbIIIbFvsZ7ZxuwN4HTJjlFJKygyHamY7pQrXlldwB71YRkDBBgIXqHU7+Hxx3L4+ob6AJEpUyyXs7rZu7GJtGzPUGC4X6LUrLBUzPMwVsOyG0uvELiIuV7khBTJZrtZUd+r2ljXxt683o3w68jMXr7mgHg32drZZWV2k26kjguHh+IDoEDUW0Wf6+OwXv8IvvPIlbHYXnU4fp0cszWg/onlP8qDZbB+JOAyDE3OHSQxKdkuf9Q0nf//aa/oP2J0uFVzIWvHg10HDIx8sEjR9wnsH8c36T0hPJE9f16Jdq2vQvYQ+yShGZoBGMIwZsuGhRdDRZjzqp1etcvLwGAMjA9y+9YFuJGSDMjA6ooJWmTveufeQnXRG5VyyEJAXKxbwI2xz8dbIHFXSElwBP9limuV3Xyfo8+CSbtVmaiBoISNYG1FvezROUCBO6XKJcqtNqVxV+2mt3eb3/uB/QqJU/o9/+S9Yfnifi7JCbAowKsnTTz9FNlPm7378Y06fOYNkbHrcHtpV2XP31a3p9PiJDo7wYGUZj9PFxXPn1Uf/+mtv8+61m3T6Dfr2Po1qm7C4Ey2xJ3iwOzoaxSezTqfeLD1NLpNgqVa9rUm+I5OTMhNH6rTdjS1lk7bqdZwSpWevaFa6y+/GaQZUwleqV5Fw4F7bEOwKcXcPv6NAqFHB166TKlW4l85SbEoV5sEfMpWJ1KVDs9shGAxpTqgYCkPxGKHBmJr2utL02PraJOrpZlksP1xgN7mlUxFB8siJK/E8khE1PDbBb//OH3Lh0uM0213V/Qr4QdhGrU7r4LCQcAh5SkW5JdevdGoyzC7nKpr5J9fllasX2d5L6TryoMOWjbXtQPUj97LUm3YJZxWFkBBgOjqPkjtehAhivleepc2G2xdCgjlF6CEnkYhK3ZaN01NjPHflDJmMxH2UsXYlnbPH4vwKs3OHefvGbVY3NqlUavTkJZBT1u3BKye4JbVqX9eMMjmQ9ZbH6cGU6rdexNO20SjYNKfHHfdpVIk7FCDgdmtn2LZaWHa7Gumy0qX2bcormjt1nE99+hM69vqlr77KzWvXtIY8feoszWYDYcrbbSaPPTPVZPIAACAASURBVPYUXp+4clB/uL0TwnAZpDI5CqUiGw/uUShXOHv2AvulMhGJck5uMjk5rGqr3WQKR/8AXCsCrHbLhtPwo3Ww1cTtDWj8SDjqphuKUyjmqTXrrIhQxufGIVORRksuLBU29x0uqj2DwMAUVYfJoMdLr5Wl3S3RN/u0XE6CrQ6DHYh2mlQbJT4sVdjK1qh0bapjFbiPqHzsQlszDQyvi12B0GJXuV58cFAbWbm9ZIpjGH3chp1qscjDh4tKkXO5wSNbIk9QpZS5YpkLF67y27/7T5mcPk691VNQhdSocrroQynDf9ESyAEmt/DBVW5TWLyIGjbXd7V4lt94/v68rhx1v63f/oPdprYP8rG6ajzozmVj0xbrhAzcO1092uVD5HqXDYDUHpbVplatETXsRK0uZ6cGeOm5j2mtZ7p9mrKbzxbpZhusbKzwwcqaKuulqRJTmWwzPD6vhieJskjgo1JZmIZ0+n2cplPLCPlLr92J2ynD/J66GuV0EiW6Uwbo7T4La7vUDDtjXoPTUyMcHh3k/rVrLM4v8PyLn8Z0+gmGo/z6b/wuhS/u8vM331YV/nRv8iAvs2NDmEQtmY/qYqGlwfVDIyP0TZOlhTWuX79NODZCueGk5XHTdZt8/Ve/rgDbG/NLfPdHryviutZsKlXZZdhVoC1NRq9nUG7aMfwubRaExOsOuKmXiwfrxq5YVOxU+xYumY7UO9jsLQxvgEouT7vTxxYOMD4UwRP3Yu838FdlX17XcdtyIctmsUi500WgHWJppm9hk/BVFXEfBA5Iyp2EBcyI7tMf+CiWW05J0TqoRZ7U7hYbG6t6WwjBz2UYai6TcKtWt8dnvvgVfvlrX0dGRO1GH7fTq4xQmWII8EuMa9I4ys/ZLg/8PzyY8owJJUNsmp6Ql1y5iOl289TTT7K+tUG1LCHq8iSLiLJ3IO+XD5YTUwDxluxcDex2Q7vkA32ddO7y8NqQVNhGWfbUVeYOTTAe81NP7zDkHuTh4hJmMEoql1WRwvZe8sCCK9dzv6vzwF6njcvtJhKOqLpe46t7XaRLlhQN+VxFBa8Gur7MDd1a+4nGz3AefINl3ib0h4qnRtswaXvcJIbnSETHCXv9tHtFHnnmOR5/6gVefOHjNLp27I2Wrsi8Ti+XL19ke2eLy1cvIfhA0aI+eLDI+tou5UIZj8/UTVYxm6fbsMikBZDlo9SyeOf62wwejtIo+0j4wwxMhLn6yGP87P0PWdjawe0PEouNqyqcjtSVBw+PWJeL1RytXIZus47pNfD6fXrVR0dDVBoOgqEx7DToynKi1UY6gUZ+X31XXZuD7VyRkKPPkFUh2MyRb7XYFfJvo4ElWZSWpBz39JSW+bNPIFg9i7KuXV3MzUwzKHpO06lq//+/py8Nsuwsz3vOPfty1+7b22yaGc2ikQZJYyQkhIOBGLMYBzDYTiqkcKAwBmzHArvKcSWVSuVPKv+SVLnKVfmbilOVqjhesQMOmFVCgBjNSLP0zPTed1/OPefcs6ee9zQeakASo+7b937n/d73eZ+FZ4V9NQsRcypvv/kWptMBdEOBZ7qwDVtsF5nU3Frv4POf+wLe/e4Pi4yGwjnmXv7Uz4ozCqEn3nTSAmY5omghRYhrbkZxwmYpzVPoZYHpYCgutWcvnMOn/sWn8Md/9N8wnwYgy509hZxoGb6r6DiK7bkK42TFA8Injt+UIDt5dgxhdy0NH3zpBm5cfxz333wD8doKdqchbh7cAVMkKNSKUtLbSjQtD0rKU12rtDfcOmm6XCcUsFEbbhiWTOlkManc0/MQaro4E/P54ZvM/pcPC310+HTeo932ShfXX3gR7TNn4DbWYdccDBdLzKMIV555HmfWulB0U8getSIRc9UsM9Gud+FcbAjiysxL08lx48YzMk0f9KZQCp1ZI5gOaWVtYDCdwTDcitScL3Hw8AjO2fN45c4b+NZrt/BzL7wdb79yCY+te9Dr63jz4QwTQjE0jFBUxP4UGU1baWMY9JGHc6SBAeh1FLUCfaZcNE+JD6nreLDaHkiKXvpLCbEyPAPdlgZl3kdjPhE46SDw0QtjRCUHRQsmciSOKqwq3kgU7vDj5eC3eeoxrG+chsMekGYFjIhmJVWpNqhhPO7h3vY9oTi6lJMYHGR14fL2B0e4cu0afvvlL+PS1esIg1L04rpJX6dKX8aTqJuaEMWlWOeFKG8jPziRuyhsESlSj3Dn/h3cuvsWNKMB+uV873uvgRWM3DlFCeTu5sk+qbTSB1R/zc7z5G6nuwSJn0y6QgY27dcun8ev//OPY5UJEq++hrGf4nAwgL/ch2E5cqBcOr/5jB1eiPm9pjvi1Ms3gbQ0am94ZTKrW8RovILIgFchuBqnQb4CHkg+FNxGkI9IUupkOEQUB1BsG51zZ7HW7uB8q82nEfdGI6mq02mINcNFMQllOj63voLVbhNlvMTuYV+oY+O5j2mQiRdT3QBOrbsCm+VqiXkQyVP/YDjA2tYmLl+7CK/VxN17d7DZWsXe7X28eOVprF028H/+/Ov4v4sZ/OUcVy9ewM7DPRzdvYf185cADhx+D7rKQ2pJ756pOuZLLjJCWespmgl/nCCk03BjBiQNLLMYZZKATCTddrDqatjKxyjjETI1xe50Bp/ZeKZLxTlKqlUzipXZ/gAFs0P9CGlNxeWnnkHT6UjrEiZL8YxnWhkrm6oqkpN0eLCDpmeLdTg5to7pYTIbitv0xz72K/jMZ74E221LNqShs0Vhu8UL94T4o/KG1quQ1TjCbDqTtTLnlErNcMJgz2BgGATYO+qj3lAw8UdCEuYQwghjTkqEBarTWJ1O7n14GMSDm5WSfEtdRx4HQuZgWsXPPHUZn//1T+HOm7fxJ3//LYzmC4GmWLwZmE4YKilL2ZdyerMtBzbZPoSdiIdCFWczusgt06Xs5lkJuS60HLbq7C1Jz1dExcedPUmm8XIu1jTT6VxeCxt5JSkkTm9rfQ22psCPKaYaAnZd6G+uWcPeyMebD0fi2ehpPgbHPUyDBdpWJsMTNTEr9bqQfo9GPlY2TmFBh2U/hGLYkkzmRxNcpz10u4dHb95C1O9Bb5f4/g9fwYWtNjot4Patn2CRZGAaW062DlPTxvvS0wMhWWfIGTI1mYhRGLiFYg9IpU2hwdFcwWLj4TFKO4DOFQ5bKivDhpGjNaXvUAqfYal5jHkBtBpNYffLyrjkrk1BjStFMcAqxfKRVMcaDLlhCBNxycA/z4O5jBcSNEC+bqfTlBuJeC8/w8GwL7Ywv/mll/HhD30SeaZJiBfbKm4B5SYll0IhKZw21oXEusTBEpPRGMPpGEvyXiPCionAjjLp00PSaTTx5lt3sbaWwnYcfOfb35W1nKgahSPHq7vSerNq8VdVQUv5QXhtmqYtwVQkyrbqTXzg/e/H//7TP8Wt22/BdF3JpVEJmrLVlU0SoQFqeUpxv6g2LurJEKNLykSWJIiTCJpZebbzQ+SDwlWoCJdqQpTHkmm304nYmERRImx5lbIDyxAeaNvxcOXSZTEeYKjm0J/BzHMhr1w4dxp7u/dx8+ZDlGUTyWyB7cUM33rlx8hU9k0qGg0Lj2+u4LknL2B9tS4yCVLRbjx1Sb7nvb0j1J2fxaVrl/DVv/qaeA61umtIfB/1hoGjw4dQihmuPnMRN955XcD0Tr2NS1cuw1/6OH60g+9/+1XUaibyTJU9cqLXkDqaaPKRqjKkkrFFi+slneSYUc7YFlOVoIJ2GGMjnCEzMgySDOMgBTvPbmsDKMOqj5V1MtsyQCOZxHTguk3U6NWelZKvJOVNTOFq8tAMh0fYfvCWDLWd1ZVKZp3G8MM54slAVI4vf/kPcfnKk7Kl4nFRKRynLWJRg1JyIK6KmMlFCHL4rOKTmVg1BnQdltzOE34vcUxWn35vKM5jTH+g6IpGSke9YSV/JaQi2h0Kw04OhRxUXuvVRkckjLVUrKhVi5J6FVefuIzvvvIDiSFprnYEdxTMU3pAbn94QKlALAX114yTa1nTwLD3hJojx5OqTF26cfI9KxBflatmEfnY2XkknE8eRoLAmbwJukh/2Y/y6SGR+cknn6xoebRmScmc13FhtQXda+EBlY+HR5IJtJjOJRn2wWQi8EsGDY9Gx2j6Jp4+fwouErSoT7/+lMiMkUY4f2oD586exU/efIDheIY7t97CcBKgtXUBhruBeTKD5zhor15ATanD8Dz83Id/EctFKluj0xcu4emnn8Xmuau4u93D/t4hRpMj2HUbcbZEPpuhDGIZ+Mi0mkaRPNBMnHVrKi5YDq66Ngja+7MI0yDHNE/QaLXR1B1ZPszDCi1hcWH7Rt9Ou05XEwc5nYZj2gDVqgNV3Y1yPh88vI+jox14DVd0T7yxBJMOfczDKT75iV/FF3/j99BsbiAMEzkzPFNsWOVGrfBybqrFXIGap9FogmGvj4jBqMFcpCq0kKQ26qcXs8amlrvlW7e2cXQ8wP7+uBowdAc83SW4IyUyTzdfExn35KycJAaf4JlsIRSyUOIlvztU20GYZdjb2xUOJekfZI8TEmCfwV6F5A1dHIhLdgGIYmZR8p9VmnShdxBFJ6bGN4yPHNXXWSZxety2kDLFrBquP4VSpxvy7/MN5m/yJmkzfe3J67h48RIGgz421klq8OTaZfKXYdakIrlGCzvHhxhM97HSdqEmhJxMTP0xzHIJPTXhmTY21toy1NCymT4OjsZbgj9hTbRCw+kE169dRqEYOA51cQAuw4EYJPzkdpXaMPPH2Npq4X3vfRGdbhO7xyPcvnmI3b0Rjicz3Nt9iIbnou6sQSfqsEKLuDmW4x6YM87NT10zsbXSQjtLcFbTERzvo0ejisyEpjnwDBO2zj18Kl7sbPx5KNh/6zVD4r7zmoIlc6o5zP7DAkUVkRhx5e3tbQThTNSiZIjxGqbMlu8jpcT//j/8R3z4g59AvmQxoUhNk2GK54MEGGnJFOKWFYTEoDI6Sg96PQT+VOIhabZB5IUOMIVZFSp+zhoTBgajAb75968iDLmC4pusyvqNQDmnHU68zBEUqEaIHCy5bGRP+k5uXYincbIreFhKHB33hJRBMLqWaxKpwacoV2pyeHjO4iREVqjisciUrjp5gbVKXktyCFeZJD6Q3zhdLAQq4RtI4q8cVo3XDwklfNMI/vPrs7FmX8QJjBsGBRfOPy5Sg8cuXKhkExqN61WZuqfzEFlJ9CDH/v4I0zTCzXsP4OktkLhy/PAuTq9u4LB3gHuPHuI9z54V3/OE0y2/v1k5URzuPMB40BeL6rV2HT//0nP4X3/1LYxHQ5gKB7gMMabIDA2dpoNTzTqubK7ieDbB7Zt3sJjmGAxGmJPV3azDaW+gprcQUndLDNZ2BO/zCoYPuLhYd2CHcxTzIXqLMRippbottC1PBHa02uEGpCypUC1g0nlCU+R20Wo6wjgFISX6mbJI8M+oigqtqOHocBc7e/fFanB1hStbA6VahQ2MxxM88cRT+NKXXsaNZ16CP0ul16/p5E+INFHAd5LGNWSo26pk/YSMbhlPJQV5Pp0iCGaCbVuWWbkF1kpBffg5nhxMDUe9QzCrkOeMlYZFmEQLFkT+vVRHYpJSxtjMMselgnTYx9GYi48drWXKJY1BDQluV11NuHqOTTCW2GQhTxWDVYP5Qg6w6Tarakh4h9KKkhbNKeI0kt0uN0W8PggEC0mEHapSE1tm8hVZ+/mA6BZ7Tj5UfJsLMWglacFQbZw+dRYXr1wRaQWrHBlPmmXASmvYORzi1u1tDPePsJj6sFa7ML0V9PsTxMLqCbBUZnBRIIpDfPXV1yVT853P/QwurK2jN5ii5pmYBCHe9bMvIlxMsHe4j69949tw1Bh1lV5QhmxSwkUEv+fj9OULQhn77o/u4mgwFGuY/eE90Fiq6TZRunWkdQ9UPc39EEZWQ3urLYhCs7sJd3SAsr+LNAkxXsaIoQsH06m7sppV2PpYlvhX8qGlDxUFgMSvScAh0VD+mwuQE50W5SIkZW/fu4WDyT7qTReeU4dYwNQUSU6jKezHP/pr+OxnvwTPW5GtoEhiVFXMKQgn8ubgAsRSSzTrtphB0MJ8OKTB2hj+bC4qCbrFsddkrCBvQbZdjmkIxbLaRsqRIoxVXX+EYVDwD2pytfJgMLuQTCGV4HQcC1ZJWhOna1ZKVjmBa0QPTB24inp7DbalIpj3EWehbIaynJugUiogzbQIgpMsLIefiRX+DBHtoKNQKh5xUB7Ukq61ZSnrTF730mfy/ge/Fj8+wFPr4uPOh5+bK2Ki7W4XH/nQLwk5JOAApepwnaZM/7laIExj2HUDbaOGL/72Z/H1136IP3vlJpIwgZLncGp0vY2B5RRWu4tbeyP83Rvb4iWUel2MphEcAKcun0FrbQ2eaUCJU5w/fwH45jeFWG2bNdRMXdyWm9xclcB8PBJo5eFRH5ZZQ7yY4v7dR6h7XXimhtHeCI0zGlptG1k0Qt2w8YS9hWxyiOzhW8B8iHm2xCTJ4bidKjqaJJpqJhViDa9s8mZl8WHw86lV4LWqy+Cp1yqGGKE+HoolmUV37yCM5mKjyFuS8hPeR9NpDw1vBV/4wpfxwV/8GPLUQBhyv8+yQASASw0LJXVcBS1pTIGTUrHEnotMZDqfYBH6AiEWwiKqMqI4GBk6h1RTbtKqM2VzxrBTlkaqHNmv8X/Z23HgYQXlM8AUAUIa/Ocqf2D2ACLAFEtlee4oPnIsaWC76xtor50Svx23QQ3LCASsyVtkpeJTxW0O3c9Ug/AE/YJCCanigSdUJJmHaVC9mQTMSaHjtCcDmCJV1bQM3HjpJSRZJvga5bWuRVOCyvXjuXe+C9eefVagEfoytbtNLFmZS8AsGQ1wUtE9G4PZGMf9Q/T3d3Hl8hW59ib9I7z7sRbyOMOemuDW/jEce02IKD+6t42z7Yao+8J5KGaue8MF4jDF97/7bVA/rbl1rDQ9aTHihCs4DZlrnvTGBSaj4ypbfBGgubElslafLCNPRcMt4fsDtB0DHTVH/vBVFEePkC8TjKMUvmpCb3RkG8SCwV+E1Xib8DqUgADiubwhiJDSwIDAtqAZ1QDE95rrQPaMB/u7wqVtMRCLXgBMxS0STKczPPO2G/id3/p9XLv2LKazUGJxaGghaw+RM2QCxLNfbzU9eI6FcBZhb/8Yvf4EYTgRMWAQR/JZMLCMpYNtGYsFcWgWJw65HM543AWZlqXQCQOdHzxLK8u6xtH+5DHkn2Gl4hWRxpFcCexPGedB6GZGexZVF8ZP2zPx5huvYXXzIhSVRIkEShyIOk+3LfKehX/JDyuYzoSWJpO/VOBcvIn4bhL/qjY4lE8QOa0yYniw3/7cc0KiOH/xIl588Z34r//5v+D1119HabrSW73w3NvxMzduCGuI+9lYs9CbJTCYQ1PL4Wk65vMUP3xjB6/95Cb+x19/E46l4/TGJhD5oqunA+65U+cQ5HO0tQa2BxH6ChWXGW689HZcfPw0Mn8hOF+cK7g/nSPMUiSNdRjNUxjEfTHjJybJrQm1VDXLRUz6mVrDmdNdzAZDuHoLQZHBMnUk/gwG4bO5hQY5k/MFnJw92SHyQkFoWIgdE216MtlWRarhhUy9FV2K5V062dLRqjEvkWaJDCU8sHwf+TnyN/Xt+7t7QhCxLKMaemuGyJ2XcSQ+7P/kIx/Fb/zGy3Ddtigc+PVVjbwIHl1dWidNSyU2ptFyRSU6Gy9w784jjMczxDGZUdXkTUdoDr+cW+QGJixERz4683H7dPKL7ZiI0QiiihRXCj6d2KrqmCdikyQ/RJoVMA1b1oEE0lnVNldXYCkxhosQuVoXk61ZlGG0/QhJrmAW+MJAeuqpq1CWPt66fVMMr+bLJaJFJB7i0jrIC6qaXk5+1X9OcAal6hk57BBaWltfh+c2pBK8693vxTe+8Xd4/NJlzGmRzZzzpITR8ESdSDFZzWrg0I8wLmpoKa5Q7Q4GQ3TqHsb9Ad68/wBH0ykYOq95DYxpCjWbQ8k1uPU2bvcDjJZzGFoCy1nF0XyMpreChzv0cEyxqjs433WwtgE8tr4iaRzrG2u49Xoq2Kpu12DZdSGUxFkGr24hS12MmbeT1+A2NtBSEnjRGKPZtML8mH1zfIirbRdlPBHMdUbzTMMUcH9zZUWAb74z3G2z2+cNRmIJBwNe29JnM7E4pUdU1abxMBKCZoWiDxUDY5dZhHrTk0NJ7if/TUI4dPf73L/8HfzyL/0a4kTBPGTyR0Xg5RaOfEpaV5IQ1Gk0ZH3MSjcfBti+u4ODvX3kJaG5SAoTRWxiz5NxvUnSCIdgsuAZ20IlbRW989PDKQeTf8PDKUeAh5SLek7neSb77pRTtxyYQvamtufKG0AsMtM1mXjbCq1XAoyTTN4k8aNh3G9Z4s5P3oTXMCVQMw0qq2weMu64ea3yjqmeZD5M1YKTbyKrN/99XkHsY1lpF/4CtNX+4Q9ewzve/hw+8qEPydP3/PPvwH/ffoTOSgvnn3kGSr2NUazAdlyUdQvL8RA5PNzeJeQS49w8wsGDu9jfvoekqKHbbMMuUkwWPrIswmqnI1qYO8McW4SYdANut42n1xsYHi7w1qM+JkUKY7mHt63P8IJ+QQB+2gXqSoFJ70iuadLY6A0fLn0ZElsrTXRWPFDuEQYRcstGRh6C6SFVQpxaq8MNJ+LONqHPz3yCVDXgrqyKRJYEZ674SMgWelWpVoMeF9G8wgnJkQsrcJ58stX7yKGRE6+ioNcjNPVI2F/1uiMKUq3UhHDNfvKxi1fx27/7r/Hs0y9IIBQJj+xD5YDTe5SEHTKDbJKcLViqJu3OfDrHgwd7ODw4RryMBFpM8gRt5qOLtffyH+YJR9QMJAERq+LLqlpGvmIeiarH5MjLg2A6Ytusq/RnrPpM4maCJnAPzZ5TAcIglKBO8iyDKfvHQgxA4yCURNzSUnHtyWuYzOZid0yohyZXTDAoikj6x5/CAnIXsPOQr10dSv4NX+hPDycfgKqyVtPhj1//sQxCf/vVr+Jzn/9clWibZrj+4ovQt7aw8cQzWNo2DoMQ8/59KKYlgqlxb4hFmov/5Z3dR9DLDJZhiuamuRzhkr2C14NA3vjlLJTcxXnDRTlK4Wg1FPEETceAWyvxMPLRf5hh1VRw9YyKuNCwu3+M/mSC82c3haI35RClW0g1HXa3S7BXLG4ovFvxPBnqRsuZhNFfbq2i5g/RXPhoIYVfLNFbhKjVm0ImrntNUQ5oTKcQFlCFFbL6EJ+ka3JaksKYSd8v2he2PirFY9WHzgl8f3cHx70jNKRKcmAiYaIGDiTzZYD3vvcX8Pkvvoz2yhks5lVOEZWepC9SucDMd+S8uoHWikcESjzpF6MF9vcP0Ds+wjIOBTVJ0gSddlP8TMOA54h3IdlMlHHr4kHFz593pbxGAearm1O1TPPfsVpSyciNhFOvS1tJBw3mmBu2LfgkJQyscnxRek3D6to66u02NFZSwkBOC15rVQIE6paDVoNanQARoSSSL5g3qJjQbVLqSe/KpAIKG6g6nfJwsPdilfzp76ohrtaW/BH45FFdyWra7/dFEzPxA/hpgSefeRalZqM/jaRXHNEb/rXXMCdRt7mCR7fvYrS7J14/oT/GeJGgNB20rAKrRomdwwGCTMHFxy/AVWJsugZirQZfNSRbcZYUMgEH8BGXCSzTRcey8LZzK7jQ9eTQUmW50vFguTpub+8jK3Sk9OI0dVj1uuCWh6NjRJMZ2p0ODFvH+aaBf3Shi/mju0j8OQZBgHFZwHI7WGNupwyVlN6eqFPz6kHlgEg5CL2cmOzG3pfvFz3hZeVIJ+Yaw1E1mYjv3b8DBqq6TlV1+TmSBE4khHyDT3/6M/jiF34fdMsLltT9Vx6exIRJ4q3x9soY+qCjveIKasNhbzYKcLDfw/HRMRbxQiwQY3Jomw3RUnKwpfqTn6kMryY3MtXDwFLEosSbklf7d175Dg57hyLzhqqr0JIS8YI2zqT424iDOTxbF2sT0p5qlgdKBmjM1PI8kc4+tt5C41xXXHWPpgssQ/4ApgQZvbF9V8T0cbQQhaLjrsHq0EiA+iBID0WxP12GeZ2zEhfcrVImwYUPWwoyiKTO80o/YZ5wADNtmG5dfmt2Q6Cp2XyKb9+8Jb2PYWoYH5pIx3PUea1Nj3Hre0cY9sdorzRRJBHiIAHB3XoZYTmNsZ2Qa2pBqXdw35/i6YaDz/7Ce/HHf/k1fHu6EDqbo+sY57S2scEGv94IMfHHiBcdLHwHR/05qAx1DAXnN7s4v7GKe3tTcdUtiwirwRT+bIxlWaDZbGFjpYVVJcbi7k189Ttfw4Jem4ohnNGG56Fuu+JxbvH6pM81V8A16v3J/C5ksGLvzweVvznQ8sHmYeO1K1TEEjjsHcvVTSDFoh049e485kUphJ1Tp8/iK1/+t3jxxZ+v2osig04oiAiMEDlof84NW4aVrg3HIZ2Qi48cUxqU7R9WshTKl7l9yjPUW56IFZdUiTIPSNAdgu1krkPmC36+cnFLyayqppxSucprTHNLkMUZdN0Waz7Qjat6ZfBcDw1viVj8DTSYXgPxwseDBw/QO9rBO577GfQHA/QOexC/Ud2QA0P4VDdUKCYZRyTxtGE1V5Glc6C00N24gCQOMR7SbJ9QSiXd4IxGsIAuH/xxOH7xJJtmC2vra5IGTDOBV2/fFs8jNNZwtAB+9GAEp+OigRjp6Bi3Bg+RhAWKVME4WGCZMJKlgZgthWLAcQxowRDXTz2D3QUdimnAn8FutAVzvT9M8J/+7Ps4WBiiEH367BZqWoF7kxHiNBdjW00lkUJBzy/wnR8/wGC/D6/TxFv3l2gaOd75xBOI0lu4l6bQ3BWoVhNnth6DloxxVivQGO2jd/cOJuEciyiR9Fun5aHjcXtjygZLsEJxLeNmRJWhj7v+JWNsIAAAFaNJREFUNKNyFcIpqNr06rquek9CbqpMug/2H0noAkNTFTKUlBK2acoQyn76+Rdewle+8oc4d+YJzOeRDLVs5eRAEhWgmjRlnlCJlXYdtq0jjlKJF5xN5uKXOhjSVS8U1SR9Rz3S75SaMKMKWb4QwqrgRLZwNMIgLCTbZEpweBD5QMlQJD8N4SJSx0gh04Wt7If0fkxA8TkrGCdFjmOEPEgITpdL6SEIYM+DGH/+N1+XUFBWPdOykSvczfoo+EPVHOiWAzrJzOcMt+Q0PkVtGcNy63BbnmyXAn+IoogFIuAunt/PMfgmODIUOE4bXTrlqgX2+2P0fvQTAdPpg/S9/vegem0YzVW0Gy08e64DK17gtR+/KlzE4ZjLOg2upfMxRbHMRSA2C5eA3cGtsSqh8jXMEBIHDMbouGsYqgr2UhICddSSCLT1mxcR5osI3WYdK06BxdKHn2p4a78PJ56jCHysNSz88N4jhMUSzz6+Ca/VgjmeYZCXUE0brTxFdzhEvPMW7jGNOAjFXYOmZY7rgqw/6mgIjFOagho3R+wdcyEms1LyIWO+EgMG4hPXEMtmRGE1dfNK5PW5/fAB5uEc/P84rPDhpz6f0Aw/549+/JN4+eV/A1NvVnmfsrKkMoDdJL9WDXGyFLeO7oot+qKUjiwLYrAz9BhvPRoginwEUilzNBxXCDflktgmpRv8vhqcE+6t8GW5Dha5DQ8hkXK2bhXWSoiQBVSmcm5g2C+1mm3ZhwfRHGvrHeHIzRYlkpSLfwdpsJS0sqTMYXJjkeSy6iozBSndiMmhJIGCTmKWhiyLkS55lRtYbXEPHiNV2FAD04UPx1mDsbImfR4TJWjatYgC2N01XLxyFXZRYnw0RhKk8lr2j3YxHfehZSkcthxBjK1LVzDPAVtXYOcKOo0NCVoqLB1/+ed/DV23oOqENkoswqVccwo92JFCoUxC8bA47qOtlbiytorHzqyic3oL33jjLUmMYEZ4VFi49fChZLSfO7cFrZYhHU6lzYksDb3pENlwKOFUN2/fRaQB9ZU27vgRGoUizJx0OEJzfAgn8cUuOvQnOKbxre1hs70mETYkt/B9qHQptKlhJJ0m7K6QHvl5DYwbJ5UsKxNRMVIhyupKkIgcRr7/R/0eDvd35MO3bF3uHYYpWCTXhAHanRZ+87dexgc/8DEUhQ5/EYmXEuU1Obdz3J7llF2kaLUMtBo21LKGNMrlqicbrX/ErPQpIobYxom0J416XUxjCVGxXWAl5NciGYgMdw6wsgKV1o2tSQ15Sb0S0ZmauAayBZGpXIYMbkNsW75QuFxCt230x0Px27Frpvjx1BxVuIzkJiYGredU8TlPg1B2n9WTrYPYJ5+AOJkL6ZOME25caJD/6OBAJKiRmoH0OLXVgZbnsC1PDmu9uQp31UXs2Niepihnx0gPd4QRQ9JEs90ECcjRbCIOEO3WChbUO1N8pRjo+wG+E4S49rbLGAY5Llx7Bsd7h/DzCI12B/nRRPx0UlpclyXIRFfHe0DowzYTXN86iyzz8cJT1/HWzft4tLuDLCiQuJtiANZuN2FZVF9OcXXzNAbpErZrg77iSqOLB4s5UlPFWqctds/zox76/gQXGjquz3roBFNMogXujH2kioUz62dlqBAGfp7Ihy+Z6SXbqsp5eRlmIqnmAaKgT65wzqBEKgnZWFQrcjNGtWqGRw8fYjQeyUaKWY/s73hNkh3PtLprTzyFl1/+A1y//jzmRB5IG5PrmkSc6grnrUUHwEbDRMMzpFfME/oBpDju9XB0dIDAD8VBbx7wZ1HQbDRh0WMgSYVLwa/LKui6HhzHlXaIMg1WSP7zssa+mH7r3OaroF8q0YFqJpfFG6lG3PLoYjowD0ZQdBuzYIEoVUV073J96FIYqyPImJpmy6KeldZsGMgNHVm4EJ6fMJBVVQxameqlkc5fb0tERjAYIHPX4J25AMvuwDFqGPQfSN71xsYW5jFAo1Z/MpBJ39cb8N0tJJMBrFqBeERLFO7XV6CUsYj4y7xizBAUNhwbcyPDzTdK4Sa+590vIH02xvbRIyhpIrvlcZjBdzsw6pviLx5P7uNcC7hx/jwGsYmvj0L8zz/6E5wFs2vaWFoR1lY9TPxYfMMngylOb27B1zVYXhO9WYCAVy0SLPIZVu0GFvM+diYjaNMpLoZHuBBZkn7xaD7DJIph1lfRMuuouwwuTUUrw6mXabbpkpKRGkIm6ApZhgey4sRmRYy8ZN9XWfKwQrJQcAW7WCyws/sQqdi1sC+uGGC6SkA/Rq4k+MiHfxlf/MJX0GxsiHcSD7M4OgtMU1VKguymqYjPEDdhNIHNEsCfh2J/ftw7AJN4oyQRZxAiNYzmptco3VL492SX8fs7NiUyjsCD3CbKoSTmKBs84oPVapT9JhEG+n6y4nMgEhxTCBmsIK0mrr/tKdy5c0ckmEx6tcUUCwiCCGnBlV5dDiBPehz5CLNIGOasvyT/iyMHpbMoYJkODJPRehnyZCFWxs7qGWiWi4aSoJj74CW7trGKsIhhrnSxSCKca9Rhax6+OZ0hdjbhwUF6dAdYzOQKL9mcK6b4D0XxQki4Knscf465mmE29qFqJv7mr/8CnfUNNFpd9B49QNuzobabSGIDjVYL0eQYGyseWnYKY3MDxw+HuFCMcWqjg8loichrohYwU7sUb8h8GWA1NxCHOZJGHUe3HmJJDoCRCUGZMoPRlEB6iEY4x/poB9e6tNMOcPvYR2I3hFjC0AVupWQAAA1VXWFd8QPjio7rX/IbeRnyg6alNXFKGs9yM6OTNEN+LE0SlBIHx1VeJQEM6u4TBoBxdtD1ymDWdfC5z/0ufvUTn0Ge8+peyCAnSwsannFQERsf8lMVST2zbA6g9AEAZhNilHs47h1KP5kUKcaLalBaabQEPiTRhkMNe8iffm+mofDr8pDy2uYlnbGHJC1RNyoZMDdVlHjUqihAbizlfWAvsNppS9b0d7/7AziejcP+CKQlNb02FssF2HOS8qDqLgqNqWAZCoZEMWQomFZ6E+JSAmfUYKsuNrrr8mTT6liIIPWO0MbicAQzG6PhqVCiHE2rgSxd4vT5C5guaxgtEyS2g/l4wrsDJt+ZYIaUKRSWKWq+LA5gMRZFyWDwA87pab6EahqCWZblAq3VNezvLnBwFMBzpnA8C1ODHyuVeikyfwhlOUWrZeH01hk8PB6gLBZ4+vJlbA8U3Fwc4MnzW9jw1zALfUwXgWjVJ8MBtMBHzaTzWiEelKxKXrsLP1vCjSZojebo7t/BxbaNYWBgezBAd30Fm8SIC1X6XEJa7K2IQBAEr/YdhbQ/pOZVPNUMCb2iiPNJlSEmKR5rkjFJAHuPU/d0CBJayFlImOYmikYVCz+SgLCXv/x7eMc7/hEWi4rfSiSBODXxTVn1ZtQSlaBvZ71tCKTECpZGBaZjH492dkD1Y5IuhUfB9onso06zKVAgeRXEsnkoCfdwPSpEGrZ07AGyvBKkEc8iX5akIJXSGQMpfeQVBbZpV9us6lxWUzmnYEZ2sNzuHExQ6E1oZSQs45qSoaQIn2zxOEUa+RI+5DRs6W0SrsEoZyghZZtObnRp4FO4TBJsnT2HRHeEn0nmCd3PoizBYZCjY3nw9Bo6NB8Nlgj9GFdOX8Lrr/8AecZoeh21cCEH2lk7Dc31QMludryD9VULK2WKe/f3ZGOlOy0ap6PMI4lVnoz7UK0OdJMPU4mQaQ+GDWU2R0oSxcVzeObpK5geH+Lb97ZRX98Cijp+cNcH4zr1RhejWYnUUvCgt8CG4eH6pVP4fvIWAj+FlwbwznRheWcQ6gboI1nfm2Lj+BHWZ/totkzcnQdYaglOnz0HW7Pg1WpCJI7LHJla+b5XTsuEZFghK6+glFVG5EgVfY8Gt/zwWCbJUeBfMr2YvE/uunn187OrpQVIxshyarQjvO8ffwAv/6vfx/r6GcwowaY6UadXAlWPlRdAQt924qqegWaLMdCK6MCZujzs+2JmMJv2JSSB7z3lE3rNks2fMJAE+qkCIqqHp9JicbZgdWRfzLNBRnu1diaJpBSNuZBO6NRikEDCK17Gpapi8k6fzX1YJftGUkgrlwliZjGrFeECy0BJ84A4EuKoa1oowhmWmQLNcCURN41K2I0mumtN8I3NjQae3jyLldPruDebw12koINuMhihZG72xjpWmjZev3UT+7crTQytCHfefAWT/QfiO0nMgGvDGulxugev3gV1Pu7KGvaOd5EnARTLgOk5UsHjYCFxLJbRRi2vwTIsYbiTAc4HjFHXtSSEa+iw6Z5cahgpFs5ffwd69w8RDHrYbOm4urKB7+2PsNcfIrczxJqB+SLBj16dSeVbjo8xSgK0jDNoNNrI5yOcQYRGfIg2pphqOe7HKdx2B2umBZ2+8rZZUcmI0xI6ohhMVP1k8qdC3ePGhu3SklsSjgTcT/MTESY6SdYV0L139Ag0FeAXYcWTcso8eRpFMNhVAT77uc/i05/+TTDW1PcZxVjJU3ggebA5oMoGTqmh2aqj1WQFy5FFPNQphr0pdnZ3MZ4OJUmOTiuLMBY2O6MLWfl48PiL34+ogMBVlMLwBhAz3gwKITjKPkmnZMsgzPZKlkL7SZolcEXJYpqyL/6HislXmadYTAdICUbymxBs56R3so0hXsZrR64RtQbLaggRN+KLMJtivJSQa2cAK1euQCtrGPXmmNKVYnsP3uYpzJIY/cEMl86exdsunca5DRvb2/cwHbbRG44RBUMczQdiI8NrZT44wpLTtlMXl5CassRy2keaB7BU2t/FYnFHxI1+4AWrhU67ERMqhVC1HHm6EItEs+ZBiVLk/BBdF45tYK3bxf37u3BWu9i9u4v+9iO86/mrmCgz7AcjXG64cEwLd3d2YIj1iYXpaIqRP4DhOOiuncLSj5EHD3E+9fH4ciSv7WA5R7/I4XRX0WKVZGoYcwVphKWRcJHIVkU08/TRiBOkRSny4yxJRY/PdR3XxELQlkOUi13iIgwwGB5JFSLkwxBW4pXcYG1tbIKOxavdLr7wpd/BBz/wCUREFPJIJneUjKjgZ0opCA/lUriZzZYhPAd+r2ypiha8d3iM3d09jGcjGcDYTrC1ozcmg17Z+7KIsRFhKygnneQb/iUna4UVnIdWgez4SzqiUNOVn8h3Sa3k5M8KThlP7cTyp2oHeMAFx+R+VZ5R25CVmmkpSKIQhteSo80XQbo8NR0UsituV8w5HUoyDQ+tlRV0GwYO7r+JeDDH3niMNNXgrtqoGTp6t+/LNLm1auPspoNOnZxO4D0/+y585IM/h92Dfbz+xm18/f99F9EiFjZOrVbgsa1TIl3I8hDZYoGkUFAYvPBSWXnNRsRJE8Q5c9Y9oWWRBsZHmD80Ne/EMfOlj4ROvltnoLU9hPkMh1Efib+Em5fwD3pQiU3mS2w6Ls46DWi5ijtHe/JQXHnsNO4+3EWIAGc2zuHK09cRKglqw32c7h/BGx1ivpxifzZFXDPQ7KyKCI9yBmrlc7mmKiEdPwTDVIXBTp4ql650UqMXk6abUj34QfOg8HKjxzk1TMNRHzv7O/DqjuReBpEPr9GAZ9cRp6Fs6p6+cQO/95U/wLUnbmDh5zIgEcdkbie13pRBEEusqQVsXUeTuiG7Jr6UtIlkXGBv/xijYV+me/qkE/ahS1zdU6BToUAHZ1a3pMoqcl1y+Dms0XvUFIc5YpWO4wgTjQeZwxrNs9iftNpN6Nws1iyalyBJFjA1B4vhgVRZ0dBwCOTppDg+z2JgpooqT6+3kFk8VEwos6R/4U9JGjxIgj11AYZRQpsOUS4WSEcHcL0VyTZvWDWMNRKKyW900R/34KoGupvreM8LV/Hi02extdJAl9JZzUAWpWg3HOzv7uK5Z5/HX/ztt8TjMitTjObjKgaFnMOihGV6KBl9YluIwwWSjFcdlZx0fYul7TAtB4VKlniOTrsjuUCqV4e7volZmomhwrVGE40iw5vjXWzfv4XuSgdbp1u4fXAXT128KtZ+O+ECQbyUJz2YTkG6WrO7io3z51AUC6zvPoR1+ABF2sODZYC+n8A2yUt0K0sUwj8MQlC4Fi1OhFaVdonJDDTC5UAZUxSWU6agycaLh1L2OmR78a+LAvt7O+gPj4WWxoGHLRY5sSSnrHW6SPMI73vf+/Ern/wUWs0NzGeJGEHwAArVjUmexEWpyUIqeHSjTlkvt8EKkiWJHBH293ax82hH/EJpV8UE4ppmCW0tjULkcSyubNzL8ytRscBf/DzYFpgy0BH6yeB5FuZzTuqVhMKkexxtYXRFwHxLcySHc+HHEte3TLj2pCFCBSfxYRA0PuVCOy6RhwvIVrCxDtVpI1ct5CbEA5Jkz6LZQKIbWPaOoRzuoalEKGwb33v1AeoNG6MEWLDvbHbRaq3h0ukuFkcjXDx/DuvdVVAypBstxKmDwSSQ3mMQ1nD2iefwoP8K/DwHvRX9+VKkr2DSa7SUBK8kXMJrtzFZhnItML6P1wOvBd7SJuWjNVOqFo0a4HaQ15nEyepDzIwqQB16qODBnR9LnF6TKRAtWxYMlrGGo8wQfmFTVWGrFgasAhxEHAdb601cqy3g3/0xjHEf9KU8DkPMSwVuvSv7YY3KQ8pmSU2Tj416bvbn1TaETCAy0fOCAi5CK0yAqLTavCK5YaFwj684CGegHcvEn0GTykSpdYjDoyM59PGSAL+Lj/3yP8PHP/pP5eumtL6mqIvnnFclSb0SFpZAsUp4rQb5xtWvTJZDCOexGK6S+1CmMQJWQ26lFBVNSwM5tByAOdBQ6p3mRYW0aHTUyxFkUWXmm2Yn1DZIZAwJJwkBroybb0JdgBKzlaBteiGwGzOKSAhhH05Pdq5DWYSU7nq75NPK1DJeG7wCFdUS5jcorajpstLrtFawutLBcD7CYDJFNp3iVF1Dq6FjGMXCdhGaas2C7nXEvXdz/RTqDQ2T4Qgt00HDVrDaboApDuxZSBLlCxS3OE3D3t6BmDVReDYajAWzy5JQMrcJswhGRosYyxIgVkBcj1uFHOmSmeF8rYz/o+21Is50btNGy3WwDGM0Vtck3GnF4eZqgXuPHgEmNUK6hA1Ml4kEU3EDQTqfB8gVZdSbWJIQjRjOoAeHuGIRYxwsxRqGA0XVUZWioeZhI5wiFC8ydJQT/TYhNTmUhdxYBLh5C5FTKXaNsgGvkiXI6BqOeyLu4v9HKx0GgPHTrYpKRSH7+ff/Ap5/7iWEi6ryVlBQRehgr0f8sIJzUth1C5ZjVCx3spLiUsIM6HbMvCPCdsRW06IQmIobOaIAnEGEXENiiADkPGQcU6pH7+SYS3EQ3iw3QOwxVb6OyvlYOWGH0WCBrCcyl4jQBAum8JLGqEn/+rd//zVBG/4/XMIvLuRiXOYAAAAASUVORK5CYII=[/img] Вон Ху Лиай Но в моём случае «изваять» диораму из монолита эпоксидки, а это учитывая планируемый размер: длина -760 мм., ширина — 320 мм., высота граней — 120 мм., что в объёме составит почти 30 литров. — Это слишком КРУТО! Жена проклянёт!))) Источник |









 . Я сам подумываю в будущем о создании чего-то подобного,- поэтому интересовался вопросом.
. Я сам подумываю в будущем о создании чего-то подобного,- поэтому интересовался вопросом.