Построение мозаик в стиле Мориса Эшера
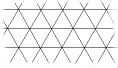
В геометрии под мозаикой (паркетом) понимают заполнение плоскости одинаковыми фигурами (элементами мозаики), которые не перекрывают друг друга и не оставляют на плоскости пустого пространства (иногда мозаикой называют заполнение плоскости несколькими фигурами, например, правильными многоугольниками). Обычный тетрадный лист в клеточку представляет собой простейшую геометрическую мозаику. Элементом здесь является квадрат. Элементами мозаики могут быть также равносторонний треугольник, правильный шестиугольник, произвольный параллелограмм, произвольный четырехугольник. Можно придумать сотни, тысячи разных элементов паркетов. Некоторые из них изображены на рис. 1.
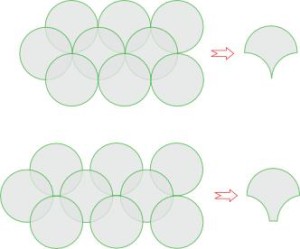
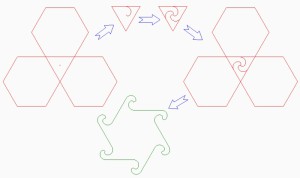
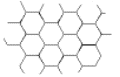
Придуманы мозаики, у которых несколько элементов образуют фигуру, подобную элементу мозаики. Примеры таких паркетов приведены на рис. 2.
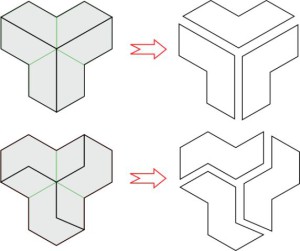
На рис. 3 приведен элемент простой мозаики, который разбит на рисунке справа на четыре одинаковые фигурки — элементы новой мозаики. А на рис. 4 показаны элементы новой мозаики, также состоящие из четырех таких фигурок.
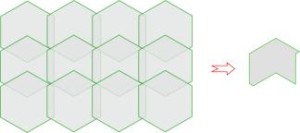
На рис. 5 приведена мозаика-паркет, элементами которой являются одинаковые пятиугольники с углами 90°, 120°, 60°, 240° и 30°, которые получились разбиением правильного шестиугольника. Из этих пятиугольников образованы фигуры.
Всего существует 17 видов симметрии сетчатых орнаментов. Они схематично показаны на рис. 6 и 7. Первые семь из них (рис. 6, а-ж ) допускают создание интересных мозаик без прямолинейных контуров.
Мозаики являются прекрасным материалом для интересного и содержательного изучения геометрии и некоторых закономерностей расположения фигур на плоскости. Визуальное представление и необходимость решения с виду простой задачи занимает как детей, так и взрослых. Составление своих рисунков мозаик может стать как профессиональной задачей дизайнера, так и уроком для школьников.
Одни из самых знаменитых рисунков мозаик придумал голландский художник Морис Эшер. Элементами паркета у него служили фигуры животных, птиц, рептилий, находящиеся в определенном порядке по отношению друг к другу.
На рис. 8 и 9 представлено несколько фигур, получить мозаику из которых можно геометрической операцией параллельного переноса. На деле это означает, что фигурка смещается на некоторое расстояние и как бы вкладывается в предыдущую, не меняя своего положения. Если в качестве меры растояния взять 1 клеточку, то рассчитав, на какое количество клеточек нужно смещать фигурку вверх и вправо, получим два числа, определяющих вектор перемещения. Для школьников интересно проследить связь между параллельными переносами и векторами и возможность разложения каждого вектора полученного векторного пространства по двум базисным векторам. Для взрослых — поиграться с неправильным копированием образца. Изменение вектора может привести к получению интересных мозаичных рисунков.
На рис. 10 показаны заполнения плоскости различными фигурами, дающими полностью покрытую плоскость мозаики. Эта мозаика отличается от предудущих тем, что для заполнения плоскости образец нужно не только сдвинуть на определенное число клеток, но и использовать зеркальное отражение или повернуть относительно некоторой точки — центра симметрии.
Общий принцип построения мозаик из сложных фигур (рисунков животных, растений, объектов с криволинейными формами) с использованием различных видов симметрии можно описать как постепенный переход от простых фигур » по тетрадным клеточкам» к более сложным. Начав с простых квадратов и четырехугольников, постепенно усложняя и развивая фигуры, получаем сначала примитивное схематичное изображение, затем добавлением деталей и скруглением форм получаем детализированное изображение со сглаженным контуром.
На рис. 11 и 12 представлены элементы мозаики в виде фигурок животных и птиц. Примерно такими же формами оперировал Морис Эшер в своих знаменитых рисунках ящериц, рыб, птиц. Далее представлены мозаики, разработанные в таком же стиле. Автор рисунков — А. Цукарь. Используя представленную информацию, создать свою собственную мозаику в стиле Эшера может, в общем-то даже школьник.
Мозаики, подобные приведенным, универсальны по применению. Разработка мозаичных элементов может отталкиваться не от форм живых существ, а от различных объектов символики, техногенных и урбанистических форм, пиктограмм и прочего. Одним из факторов популярности мозаик Эшера является их способность заставлять зрителя погружаться в изучение подробностей рисунка — от мелких деталей к крупным, от восприятия в целом к сосредоточению на одном элементе. Разглядывание мозаик — отличный способ расслабления и отдыха, приведения мыслей в порядок, и даже медитации. Декорирование пространства мозаикой собственной разработки — это и дополнительные возможности формирования позитивного настроения путем использования конкретных образов, формирующих положительное впечатление. Творите на радость себе.
Источник
Мозаика эшера своими руками
Часто люди, впервые ознакомившись с творчеством М.Эшера, считают его математиком или программистом. Такое мнение связано с кажущейся сложностью получения абсолютно одинаковых изображений, взаимосвязанных друг с другом. Конечно, следует отдать должное таланту художника, сумевшего придумать свои картины до компьютерного бума. Тем не менее, многие варианты вполне просты по своей реализации. Один из методов получения подобных картин уже описывался ранее в статье: Мозаика Эшера своими руками . Сегодня рассказ еще о нескольких вариантах.
Самым простым способом создания сложных узоров становится регулярное размещение простых графических объектов. В зависимости от степени наложения друг на друга, можно получить самые разные варианты визуализации. В качестве примера ниже приведены обычные окружности, хотя фактически можно использовать и абсолютно любые замкнутые контуры. Требуется только разместить их в узлах какой-либо сетки и удалить лишнее.
Получение контура на базе окружности
Еще один пример получения взаимосвязанных объектов, на основе вышеописанной методики, основан на правильном шестиугольнике. Но шестиугольник сам по себе уникальный объект. Его использование позволяет получить множество интереснейших изображений. Для этого достаточно соединить три фигуры, которые создадут новый элемент. Если этого недостаточно, можно разбить шестиугольник по каким-либо осевым линиям и получить более сложные детали.
Получение контура на базе шестиугольника
Фигуры на основе правильного шестиугольника
Все предыдущие варианты использования шестиугольников основывались на плотной сетке, следующий использует несколько иной принцип. Для его получения необходимо расположить фигуры таким образом, чтобы между ними остались незаполненные треугольные окна. Эти окна следует поделить на три одинаковые части, каждая из которых должна принадлежать одному из образующих шестиугольников.
Получение необычной фигуры из шестиугольника
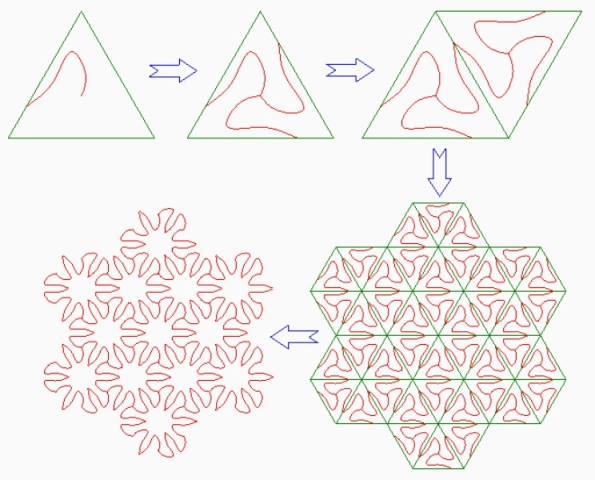
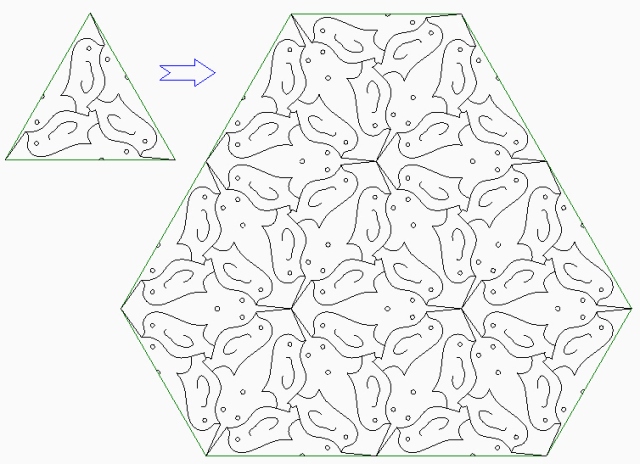
Несколько иначе строятся изображения с помощью треугольников. Очевидно, что наиболее выгодным вариантом будет использование равносторонней фигуры. В этом случае из геометрического центра треугольника строится одна часть будущего изображения. На втором этапе изображении копируется и простым поворотом с осью в центре, размещается на оставшиеся грани фигуры. Далее остается только отразить треугольник с изображением вдоль каждой из сторон, необходимое количество раз. В конце работы можно удалить опорные треугольники для получения законченной фигуры, которая будет взаимодополняться сама с собой.
В качестве еще одного примера вышеуказанного варианта картина Нарвалы и Пингвины.
Нарвалы и пингвины
И в заключение – Всадники Эшера. В отличие от предыдущих вариантов построены они эмпирически. Тем не менее визуальный эффект создают во многом более интересный. Все фигуры, независимо от направления движения одинаковы. По началу в это не верится, но это факт.
Источник
Математическое искусство М.К. Эшера
Голландский художник Мориц Корнилис Эшер, родившийся в 1898 году в Леувардене создал уникальные и очаровательные работы, в которых использованы или показаны широкий круг математических идей.
Когда он учился в школе, родители планировали, что он станет архитектором, но плохое здоровье не позволило Морицу закончить образование, и он стал художником. До начала 50-х годов он не был широко известен, но после ряда выставок и статей в американских журналах (Time и др.) он получает мировую известность. Среди его восторженных поклонников были и математики, которые видели в его работах оригинальную визуальную интерпретацию некоторых математических законов. Это более интересно тем, что сам Эшер не имел специального математического образования.
В процессе своей работы он черпал идеи из математических статьей, в которых рассказывалось о мозаичном разбиении плоскости, проецировании трехмерных фигур на плоскость и неевклидовой геометрии, о чем будет рассказываться ниже. Он был очарован всевозможными парадоксами и в том числе «невозможными фигурами». Парадоксальные идеи Роджера Пенроуза были использованы во многих работах Эшера. Наиболее интересными для изучения идеями Эшера являются всевозможные разбиения плоскости и логика трехмерного пространства.
Мозаики
Регулярное разбиение плоскости, называемое «мозаикой» — это набор замкнутых фигур, которыми можно замостить плоскость без пересечений фигур и щелей между ними. Обычно в качестве фигуры для составления мозаики используют простые многоугольники, например, квадраты или прямоугольники. Но Эшер интересовался всеми видами мозаик — регулярными и нерегулярными (прим. перев. нерегулярные мозаики образуют неповоряющиеся узоры) — а также ввел собственный вид, который назвал «метаморфозами», где фигуры изменяются и взаимодействуют друг с другом, а иногда изменяют и саму плоскость.
Интересоваться мозаиками Эшер начал в 1936 году во время путешествия по Испании. Он провел много времени в Альгамбре, зарисовывая арабские мозаики, и впоследствии сказал, что это было для него «богатейшим источником вдохновения». Позже в 1957 году в своем эссе о мозаиках Эшер написал:
В математических работах регулярное разбиение плоскости рассматривается теоретически. Значит ли это, что данный вопрос является сугубо математическим? Математики открыли дверь ведущую в другой мир, но сами войти в этот мир не решились. Их больше интересует путь, на котором стоит дверь, чем сад, лежащий за ней.
Математики доказали, что для регулярного разбиения плоскости подходят только три правильных многоугольника: треугольник, квадрат и шестиугольник. (Нерегулярных вариантов разбиения плоскости гораздо больше. В частности в мозаиках иногда используются нерегулярные мозаики, в основу которых положен правильный пятиугольник.) Эшер использовал базовые образцы мозаик, применяя к ним трансформации, которые в геометрии называются симметрией, отражение, смещение и др. Также он исказил базовые фигуры, превратив их в животных, птиц, ящериц и проч. Эти искаженные образцы мозаик имели трех-, четырех- и шестинаправленную симметрию, таким образом сохраняя свойство заполнения плоскости без перекрытий и щелей.
 |  |  | |
 |  |  | |
 Регулярное разбиение плоскости птицами |  Рептилии |  Цикл |  Эволюция 1 |
В гравюре «Рептилии» маленькие крокодилы играючи вырываются из тюрьмы двухмерного пространства стола, проходят кругом, чтобы снова превратиться в двухмерные фигуры. Мозаику рептилий Эшер использовал во многих своих работах. В «Эволюции 1» можно проследить развитие искажения квадратной мозаики в центральную фигуру из четырех ящериц.
Многогранники
Правильные геометрические тела — многогранники — имели особое очарование для Эшера. Во его многих работах многогранники являются главной фигурой и в еще большем количестве работ они встречаются в качестве вспомогательных элементов. Существует лишь пять правильных многогранников, то есть таких тел, все грани которых состоят из однаковых правильных многоугольников. Они еще называются телами Платона. Это — тетраэдр, гранями которого являются четыре правильных треугольника, куб с шестью квадратными гранями, октаэдр, имеющий восемь треугольных граней, додекаэдр, гранями которого являются двенадцать правильных пятиугольников, и икосаэдр с двадцатью треугольными гранями. На гравюре «Четыре тела» Эшер изобразил пересечение основных правильных многогранников, расположенных на одной оси симметрии, кроме этого многогранники выглядят полупрозрачными, и сквозь любой из них можно увидеть остальные.
Большое количество различных многогранников может быть получено объединением правильных многогранников, а также превращением многогранника в звезду. Для преобразования многогранника в звезду необходимо заменить каждую его грань пирамидой, основанием которой является грань многогранника. Изящный пример звездчатого додекаэдра можно найти в работе «Порядок и хаос». В данном случае звездчатый многогранник помещен внутрь стеклянной сферы. Аскетичная красота этой конструкции контрастирует с беспорядочно разбросанным по столу мусором. Заметим также, что анализируя картину можно догадаться о природе источника света для всей композиции — это окно, которое отражается левой верхней части сферы.
Фигуры, полученные объединением правильных многогранников, можно встретить во многих работах Эшера. Наиболее интересной среди них является гравюра «Звезды», на которой можно увидеть тела, полученные объединением тетраэдров, кубов и октаэдров. Если бы Эшер изобразил в данной работе лишь различные варианты многогранников, мы никогда бы не узнали о ней. Но он по какой-то причине поместил внутрь центральной фигуры хамелеонов, чтобы затруднить нам восприятие всей фигуры. Таким образом нам необходимо отвлечься от привычного восприятия картины и попытаться взглянуть на нее свежим взором, чтобы представить ее целиком. Этот аспект данной картины является еще одним предметом восхищения математиков творчеством Эшера.
Форма пространства
Среди наиболее важных работ Эшера с математической точки зрения являются картины, оперирующие с природой самого пространства. Литография «Три пересекающиеся плоскости» — хороший пример для начала обзора таких картин. Этот пример демонстрирует интерес художника к размерности пространства и способность мозга распознавать трехмерные изображения на двухмерных рисунках. Как будет ниже, Эшер позже использовал данный принцип для создания изумительных визуальных эффектов.
Под влиянием рисунков в книге математика Х. Коксетера Эшер создал много иллюстраций гиперболического пространства. Один из примеров можно увидеть в работе «Предел круга III». Здесь представлен один из двух видов неевклидового пространства, описанных французским математиком Пуанкаре. Чтобы понять особенности этого пространства, представьте, что вы находитесь внутри самой картины. По мере вашего перемещения от центра круга к его границе ваш рост будет уменьшаться также, как уменьшаются рыбы на данной картине. Таким образом путь, который вам надо будет пройти до границы круга будет казаться вам бесконечным. На самом деле, находясь в таком простарнстве вы на первый взгляд не заметите ничего необычного в нем по сравнению с обычным евклидовым пространством. Например, чтобы достичь границ евклидового пространства вам также необходимо пройти бесконечный путь. Однако, если внимательно присмотреться, то можно будет заметить некоторые отличия, например, все подобные треугольники имеют в этом пространстве одинаковый размер, и вы не сможете там нарисовать фигуры с четырьмя прямыми углами, соединенными прямыми линиями, так как в этом пространстве не существует квадратов и прямоугольников. Странное место, не правда ли?
Еще более странное пространство показано в работе «Змеи». Здесь пространство уходит в бесконечность в обе стороны — и в сторону края окружности и в сторону центра окружности, что показано уменьшающимися кольцами. Если вы попадете в такое пространство, на что оно будет похоже?
Кроме особенностей евклидовой и неевклидовой геометрий Эшера интересовали визуальные аспекты топологии. Топология изучает свойства тел и поверхностей пространства, которые не изменяются при деформации, например, растяжении, сжатии или изгибе. Единственное, к чему не должна приводить деформация — это к разрыву. Топологам приходится изображать множество странных объектов. Одним из наиболее известных является лента Мебиуса, которая встречается во многих работах Эшера. Это может показаться странным, но у этой поверхности есть только одна сторона и одна кромка. Если вы проследите путь муравьев на литографии «Лента Мебиуса II», то увидите, что муравьи ползут не по противоположным поверхностям ленты, а по одной и той же. Сделать лист Мебиуса очень просто. Надо взять полоску бумаги, изогнуть ее, и склеить противоположные края ленты клеем. Как вы думаете, что случится, если разрезать лист Мебиуса вдоль?
Другая интересная литография назавается «Картинная галерея», в которой изменены одновременно и топология и логика пространства. Мы видим мальчика, который смотрит на картину, на которой нарисован приморский город с магазином на берегу, а в магазине — картинная галерея, а в галерее стоит мальчик, который смотрит на картину, на которой нарисован приморский город . стоп! Что-то не так.
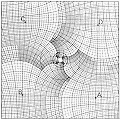  |
Для понимания любой картины Эшера требуется внимание и наблюдательность, а эта работа требует особого внимания. Каким-то образом Эшер завернуть пространство в кольцо, и получилось, что мальчик находится одновременно внутри картины и вне ее. Секрет этого эффекта состоит в том, каким образом преобразовано изображение. Понять это можно, анализируя карандашный набросок сетки, которым пользовался Эшер при создании картины. Обратите внимание, что расстояние между линиями сетки увеличивается в направлении движения стрелки часов. Заметим еще, на чем основана хитрость картины — белое пятно в центре. Математики называют это пятно особым местом или особой точкой, где пространства не существует. Не существует способа изобразить этот участок картины без швов или наложений, поэтому Эшер решил эту проблему, поместив в центр картины свой автограф.
Логика пространства
Под «логикой» пространства мы понимаем те отношения между физическими объектами, которые обычны для реального мира, и при нарушении которых возникают визуальные парадоксы, называемые еще оптическими иллюзиями. Большинство художников, экспериментирующие с логикой пространства, изменяют эти отношения между объектами, основываясь на своей интуиции, как, например, Пикассо.
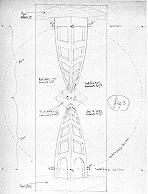
Эшер понимал, что геометрия определяет логику пространства, но и логика пространства определяет геометрию. Одна из наиболее часто используемый особенностей логики пространства — игра света и тени на выпуклых и вогнутых объектах. На литографии «Куб с полосками» выступы на лентах являются визуальным ориентиром того, как расположены полоски в пространстве и как они переплетаются с кубом. И если вы верите своим глазам, то вы никогда не поверите тому, что нарисовано на этой картине.
 |
Еще один из аспектов логики пространства — перспектива. На рисунках, в которых присутствует эффект перспективы, выделяют так называемые точки исчезновения, которые сообщают глазу человека о бесконечности пространства. Изучение особенностей перспективы началось еще во времена возрождения художниками Альберти, Дизаргом и многими другими. Их наблюдения и выводы легли в основу современной геометрии проекций.
Вводя дополнительные точки исчезновения и немного изменяя элементы композиции для достижения нужного эффекта, Эшер смог изобразить картины, в которых изменяется ориентация элементов в зависимости от того, как зритель смотрит на картину. На картине «Cверху и cнизу» художник разместил сразу пять точек исчезновения — по углам картины и в центре. В результате, если мы смотрим на нижнюю часть картины, то создается впечатление, что мы смотрим вверх. Если же обратить взгляд на верхнюю половину картину, то кажется, что мы смотрим вниз. Чтобы подчеркнуть этот эффект, Эшер изобразил два вида одной и той же композиции.
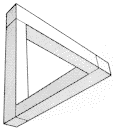 |
 Водопад |
Третий тип картин с нарушенной логикой пространства — это «невозможные фигуры». Парадокс невозможных фигур основан на том, что наш мозг всегда пытается представить нарисованные на бумаге двухмерные рисунки как трехмерные. Эшер создал много работ, в которых обратился к этой аномалии. Наиболее интересная работа — литография «Водопад» — основана на фигуре невозможного треугольника, придуманного математиком Роджером Пенроузом. В этой работе два невозможных треугольника соединены в единую невозможную фигуру. Создается впечатление, что водопад является замкнутой системой, работающей по типу вечного двигателя, нарушая закон сохранения энергии. (Примечание. Обратите внимание на многогранники, установленные на башнях водопада.)
Самовоспроизведение и информация
В заключение мы рассмотрим аспекты творчества Эшера, относящиеся к теории информации и искусственному интеллекту. Эта область творчества художника широко освещена во многих статьях и книгах. Наиболее полное исследование этого вопроса освещено в книге Дугласа Хофстадтера (Douglas R. Hofstadter) «Гёдель, Эшер, Бах: Бесконечная золотая нить» (Godel, Escher, Bach: An Eternal Golden Braid), выпущенной в 1980 году и награжденной пулитцеровской премией.
Центральная идея самовоспроизведения, взятая на вооружение Эшером, обращается к загадке человеческого сознания и способности человеческого мозга обрабатывать информацию так, как не сможет обработать ни один компьютер. Литографии «Рисующие руки» и «Рыбы и чешуйки» используют эту идею разными способами. Самовоспроизведение является направленным действием. Руки рисуют друг друга, создавая самих себя. При этом сами руки и процесс их самовоспроизведения неразделимы. В работе «Рыбы и чешуйки» концепция самовоспроизведения представлена более функционально, и в данном случае она может быть названа самоподобием. В этом смысле данная работа описывает не только рыб, а все живые организмы, в том числе и человека. Конечно, мы не состоит из уменьшенных копий самих себя, но каждая клетка нашего тела несет в себе информацию обо всем теле в виде ДНК.
Углубляясь в изучение самовоспроизведения, можно его обнаружить в отражении и пересечении отражений реального мира. Такое пересечение встречается во многих картинах Эшера. Мы рассмотрим лишь один пример — литографию «Три сферы», на которой присутствуют три шаровидных тела, сделанных из разных материалов с различной отражающей способностью. Эти сферы отражают друг друга и художника, и комнату, в которой он работает, и лист бумаги, на котором он рисует сферы. Хофстадтер в своей книге написал «. каждая частица мира содержит в себе весь мир и содержится к во всех других частицах мира. «.
Таким образом, мы заканчиваем тем же, с чего начали, — автопортретом художника — его отражением в своей работе.
Заключение
Мы рассмотрели лишь небольшую часть работ из сотен набросков и литографий и гравюр, оставшихся после смерти Эшера в 1972 году. Еще многое будет сказано и уже сказано о значении и важности его работ. С каждым годом появляется все больше и больше книг, где освещается творчество художника, анализируются различные аспекты его творчества. Надеемся, что мы заинтересовали вас творчеством Эшера.
Перевод Влада Алексеева.
Дополнение переводчика
Спирали
Странно, но в оригинальной работе обошли вниманием целый класс фигур, которые достаточно часто встречаются в работах Эшера. Это закрученные в спирали фигуры. В работе «Спирали» мы видим четыре закручивающиеся в спираль полоски, которые постоянно сближаются и постепенно закручиваются сами в себя, образуя своеобразный тор. Пройдя целый круг, спираль заходит внутрь самой себя, образуя тем самым, как бы, спираль второго порядка — спираль в спирали.
В работе «Водовороты» Эшер объединил спиралевидную форму и свой излюбленный художественный прием — регулярное разбиение плоскости (или мозаику). Здесь рыбы,выплыв из одного водоворота, попадают во второй и, погружась в него, постепенно уменьшаются в размерах и наконец совсем исчезают. Обратите внимание на постепенно уменьшающуюся в размерах мозаику. Если мысленно развернуть спираль, то мы увидим лишь два ряда рыб, плывущих навстречу друг другу. Но скрученные в спираль и соответствующим образом деформированные образы рыб полностью покрывают некоторую область бесконечной плоскости.
Иной способ представления спирали использован в работе «Сферические спирали», где четыре полосы расположены на поверхности шара, проходя от одного полюса шара к другому. Похожий путь может пройти самолет, летящий с северного полюса земного шара на южный.
Здесь мы привели основные виды спиралей, использованных Эшером в своих работах. Различные их модификации можно обнаружить и на многих других литографиях художника.
Заключение 2
Использование Эшером различных математических фигур и законов не ограничивается лишь вышеприведенными примерами. Внимательно изучая его картины, можно обнаружить и другие, не упомянутые в данной статье, геометрические тела или визуальную интерпретацию математических законов.
Закончить хотелось бы картиной «Узлы», изображающей замкнутые фигуры, которые нельзя отнести к какому-либо разделу данной статьи.
Источник