Модель координатной прямой своими руками

Создание модели прямоугольной системы координат

Создание модели прямоугольной системы координат позволит лучше понять принцип построения изображений на координатной плоскости, быстро менять рисунки. Самое интересное и увлекательное, на мой взгляд, в применении координат — это использование их в рисунках на координатной плоскости. Нарисовать с помощью системы координат можно всё, что угодно: животных, цветы, дома, корабли, созвездия и многое, многое другое.

Скачать:

Вложение	Размер
portnyagin_d._6a_klasssozdanie_modeli_koordinatnoy_ploskosti.pptx	368.83 КБ

Предварительный просмотр:

Подписи к слайдам:

Проектная работа на тему: Создание модели прямоугольной системы координат п. Чокурдах , 2018 МОУ « Чокурдахская основная общеобразовательная школа им.А.Г. Чикачева » Предмет: математика Выполнил: ученик 6 «а» класса, Портнягин Дмитрий Руководитель: учитель математики Кочкина Елена Николаевна

Актуальность Задавать положение точки на плоскости с помощью чисел зародилась прежде всего у географов и астрономов, которые стали составлять географические и звездные карты, календари. Очевидность как критерий истины: «Мыслю, следовательно, существую» Р.Декарт Создание модели прямоугольной системы координат позволит лучше понять принцип построения изображений на координатной плоскости, быстро менять рисунки Система географических координат широта – параллели, долгота -меридианы

Цель: Задачи: Расширить знания о прямоугольной системе координат и создать ее модель Изучить литературу о прямоугольной системе координат в различных источниках Написать реферат. Создать презентацию. Изготовить модель прямоугольной системы координат

Французский философ, естествоиспытатель, математик. Целью Декарта было описание природы при помощи математических законов. Рене Декарт (1598-1650) Автор координатной плоскости, поэтому ее часто называют декартовой системой координат.

О – точка пересечения осей х и у , начальная точка системы координат. Ось х – ось абсцисс. Ось у – ось ординат. Плоскость, на которой задана декартова система координат, называется координатной плоскостью Пусть А – произвольная точка плоскости. Проведем через точку А прямые, параллельные осям координат. Прямая, параллельная оси у, пересечет ось х в точке А 1 . Прямая, параллельная оси х , пересечет ось у в точке А 2 . А 1 – абсцисса точки А А 2 – ордината точки А у х О 1 1 -1 -1 2 3 4 2 3 4 -2 -3 -4 -2 -3 -4 . А А 1 А 2 А (4; 3) А ( х ; у) Координатная плоскость

Создание модели координатной плоскости 1 2 3 4

Рисунки на координатной плоскости

Вывод Самое интересное и увлекательное, на мой взгляд, в применении координат — это использование их в рисунках на координатной плоскости. Нарисовать с помощью системы координат можно всё, что угодно: животных, цветы, дома, корабли, созвездия и многое, многое другое.

Источник

Координатная прямая (числовая прямая), координатный луч

Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.

Данная статья посвящена разбору таких понятий, как координатный луч и координатная прямая. Мы остановимся на каждом понятии и подробно рассмотрим примеры. Благодаря этой статье вы сможете освежить свои знания или ознакомиться с темой без помощи преподавателя.

Координатный луч

Для того, чтобы определить понятие координатного луча, следует иметь представление о том, что такое луч.

Луч — это геометрическая фигура, которая имеет начало отсчета координатного луча и направление движения. Прямую обычно изображают горизонтально, указывая направление направо.

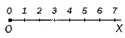
На примере мы видим, что O является началом луча.

Координатный луч изображается по той же схеме, но существенно отличается. Мы ставим точку отсчета и отмеряем единичный отрезок.

Единичный отрезок — это расстояние от 0 до точки, выбранной для измерения.

От конца единичного отрезка нужно отложить несколько штрихов и сделать разметку.

Благодаря манипуляциям, которые мы проделали с лучом, он стал координатным. Подпишите штрихи натуральными числами в последовательности от 1 — например, 2 , 3 , 4 , 5 .

Координатный луч – это шкала, которая может длиться до бесконечности.

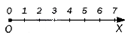
Зачастую его изображают лучом с началом в точке O , и откладывают единственный единичный отрезок. Пример указан на рисунке.

Мы в любом случае сможем продолжить шкалу до того числа, которое нам необходимо. Вы можете записывать числа как удобно – под лучом или над ним.

Для отображений координат луча могут использоваться как заглавные, как и строчные буквы.

Координатная прямая

Принцип изображения координатной прямой практически не отличается от изображения луча. Все просто — прочертите луч и дополните до прямой, придав положительное направление, которое указывается стрелочкой.

Проведите луч в противоположную сторону, дополнив его до прямой

Отложите единичные отрезки по примеру, указанному выше

С левой стороны запишите натуральные числа 1 , 2 , 3 , 4 , 5 . с противоположным знаком. Обратите внимание на пример.

Вы можете отметить только начало отсчета и единичные отрезки. Смотрите на примере, как это будет выглядеть.

Координатная прямая – это прямая, которая изображается с определенной точкой отсчета, которая принимается за 0 , единичным отрезком и заданным направлением движения.

Соответствие между точками координатной прямой и действительными числами

Координатная прямая может содержать множество точек. Они напрямую связаны с действительными числами. Это можно определить, как взаимно однозначное соответствие.

Каждой точке на координатной прямой соответствует единственное действительное число, а каждому действительному числу соответствует единственная точка на координатной прямой.

Для того, чтобы лучше понять правило, следует отметить точку на координатной прямой и посмотреть, какое натуральное число соответствует отметке. Если эта точка совпадает с началом отсчета, она будет отмечена нулем. Если точка не совпадает с началом отсчета, мы откладываем нужное количество единичных отрезков до тех пор, пока не достигнем указанной отметки. Число, записанное под ней, и будет соответствовать данной точке. На примере, указанном внизу, мы покажем вам это правило наглядно.

Если мы не можем найти точку, откладывая единичные отрезки, следует отмечать также точки, составляющие одну десятую, сотую или тысячную долю единичного отрезка. На примере можно подробно рассмотреть данное правило.

Отложив несколько подобных отрезков, мы сможем получить не только целое, но и дробное число – как положительное, так и отрицательное.

Отмеченные отрезки помогут нам отыскать на координатной прямой необходимую точку. Это могут быть как целые, так и дробные числа. Однако на прямой существуют точки, которые очень сложно найти с помощью единичных отрезков. Этим точкам соответствуют десятичные дроби. Для того, чтобы искать подобную точку, придётся откладывать единичный отрезок, десятую, сотую, тысячную, десятитысячную и другие его доли. Одной точке координатной прямой отвечает иррациональное число π ( = 3 , 141592 . . . ) .

Множество действительных чисел включается в себя все числа, которые можно записать в виде дроби. Это позволяет выявить правило.

Каждой точке координатной прямой соответствует конкретное действительное число. Разные точки определяют разные действительные числа.

Это соответствие однозначно –каждой точке соответствует определенное действительное число. Но это работает также и в обратном направлении. Мы также можем указать определенную точку на координатной прямой, которая будет относиться конкретному действительному числу. Если число не является целым, то нам необходимо отметить несколько единичных отрезков, а также десятых, сотых долей в заданном направлении. Например, числу 400350 отвечает точка на координатной прямой, в которую из начала отсчета можно попасть, отложив в положительном направлении 400 единичных отрезков, 3 отрезка, составляющих десятую долю единичного, и 5 отрезков – тысячную долю.

Каждой точке на координатной прямой отвечает действительное число, и каждое действительное число отмечается в виде точки на координатной прямой.

Благодаря этому утверждению координатную прямую зачастую определяют как числовую.

Следует отметить, что знак, стоящий перед числом, зависит от размещения точки на прямой. Точкам, лежащим правее начала отсчета, соответствуют положительные числа, а точкам, лежащим левее, — отрицательные.

Координаты точек на координатной прямой

Число, соответствующее точке на координатной прямой, называется координатой этой точки.

Ранее было отмечено, что к каждому числу относится единственная точка на прямой. Можно сказать, что координата точки определяет ее положение на прямой. Именно координата задает эту точку.

Перед тем, как завершить статью, следует упомянуть о принятых обозначениях координаты точки. Координату принято записывать в круглых скобках справа от буквы, которой обозначена точка. Например, если точка M имеет координату – 6 , то можно записать как M ( — 6 ) , а запись вида M ( 5 3 + 7 ) значит, что координатой является 5 3 + 7

Источник

Сложение чисел с помощью координатной прямой

Описание презентации по отдельным слайдам:

Левашовская средняя школа Алексеевского района Республики Татарстан 6 класс. Математика. Учитель: Сайкун Найля Низамутдиновна. Урок – путешествие «По островам математики». Тема: Сложение чисел с помощью координатной прямой.

Оборудование урока: Модель координатной прямой, Модель термометра ( на доске), изготовленные учителем. Модели координатных прямых у каждого ученика ( изготовленные учениками). Компьютер. Слайды. Индивидуальные задания на карточках.

Цель урока: Дать понятие и научить складывать числа с помощью координатной прямой, показать, что результат двух последовательных изменений величин находят с помощью координатной прямой; побудить интерес к изучению математики; способствовать развитию практических навыков.

Ход урока: 1. Отплытие. — организационный момент.

Актуализация знаний. 2. Остров « Вспоминайка».

5; !-17!; 1/2; 7,5; 0; !3/4!; 100; 0,5; 17; !-3/4!; 0,75; -1245; -7,5 1. Назовите положительные числа. 2. Назовите отрицательные числа. 3. Укажите противоположные числа. 4.Назовите число, которое не является ни отрицательным, ни положительным. 5. Найдите самое маленькое число. 6. Найдите самое большое число. 7. Модули каких чисел равны? 8.Найти целые числа.

3. Остров « Узнайка». Объяснение нового материала. При объяснении используются: модель координатной прямой, модель термометра ( на доске) ( изготовлены учителем); модели координатных прямых у учащихся, изготовленных самостоятельно.

Измерим температуру за бортом корабля ( с помощью модели термометра). На термометре 6 -3 -3 Изменение температуры 4 4 -5 результат 6+4 = 10 -3+4 =1 -3+(-5)=-8

Вывод: Если дана начальная температура и её изменения, то конечная температура находится действием сложения.

2.Показания приборов на корабле: ( решать с помощью термометра или координатной прямой). 1 прибор 2 прибор 3 прибор Данное число 5 -6 а Изменение показаний 3 -4 в Результат 5+3=8 -6+(-4)= -10 а+в

Вывод: Прибавить к числу а число в — значит изменить число а на число в.

3.На координатной прямой: Найдём сумму чисел : 8+3=11 8+(-3)= 5

Вывод: Любое число от прибавления положительного числа увеличивается, а от прибавления отрицательного числа уменьшается.

На координатной прямой: Найдём сумму чисел: 4+(-4)=0 а +(-а) = о

Вывод: Сумма двух противоположных чисел равна нулю.

На координатной прямой: Найдём сумму: -5+0= -5 а+0=а

Вывод: При прибавлении нуля число не изменяется.

4. Остров « Спортландия». Ну что, устали? А теперь, ребята, встали. Быстро руки вверх подняли, В стороны, вперёд, назад, Повернулись вправо, влево, Тихо сели, вновь за дело.

5. Остров « Умейка». Решите задания с помощью координатной прямой: № 1020. № 1021. -1+2 = 4+0= 3+(-4) = 0+(-3)= -3+6 = -5+0= 1+(-5) = -3+3= -5+6 = 7+(-7)= -3+(-2)=

Решите задание с помощью координатной прямой (или термометра): Утром температура воздуха была равна 8 градусам. За первую половину дня температура изменилась на 4 градуса, а за вторую половину дня – на 7 градусов. Какой стала температура после двух изменений?

Решение: 8 + 4 + (- 7) = 5

Вывод: Результаты двух последовательных изменений находят с помощью сложения.

6. Остров « Повторика». 1. Самостоятельная работа: а) Найти с помощью координатной прямой сумму чисел: -7+5; -4+(-8); 8+(-3); 0+(-9). б) Написать в порядке возрастания числа: -9; 0; -12; 5; 12; -2 л в п ё м ы в)Написать в порядке убывания числа: -5; 0; 5; -8; -10; м о д о й

В результате должно получиться: Плывём домой.

Остров « Закрепика». Решение заданий в тестовой форме. Выполнить с помощью координатной прямой. 1. Температура воздуха была -2 градуса. Какой стала температура, когда она изменилась на -5 градусов? А. 7 Б. 3 В. -3 Г.-7

2.Решить с помощью координатной прямой: Температура воздуха с утра была равна 10 градусам. К обеду температура изменилась на 4 градуса, а к вечеру – на -5 градусов. Какая температура воздуха была вечером? А. 11 Б. 9 В. 1 Г. -1.

Возвращение из путешествия по островам математики домой: Задание на дом: ( по индивидуальным карточкам).

Подведение итогов урока. Что мы узнали за время путешествия по островам математики? Поделимся впечатлениями. 1. Если дана начальная температура и её изменения, то… 2. Прибавить к числу а число в – значит… 3. Любое число от прибавления… 4. Сумма двух противоположных чисел… 5. При прибавлении нуля… 6. Результаты двух последовательных изменений…

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Онлайн-конференция для учителей, репетиторов и родителей

Формирование математических способностей у детей с разными образовательными потребностями с помощью ментальной арифметики и других современных методик

Международная дистанционная олимпиада Осень 2021

Номер материала: ДБ-856391

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Российские школьники смогут отправить послание в космос весной 2022 года

Время чтения: 1 минута

В России каждый пятый студент сталкивается с эмоциональными проблемами

Время чтения: 4 минуты

Студент устроил стрельбу в Пермском государственном университете

Время чтения: 1 минута

Преподаватель пермского вуза продолжал вести лекцию при нападении

Время чтения: 2 минуты

В пяти регионах России протестируют новую систему оплаты труда педагогов

Время чтения: 2 минуты

Выпускники российских вузов смогут получить электронную копию диплома

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник