Металлический купол своими руками

Геодезический купол своими руками

Определяясь с проектом для дачного строительства, прежде всего, оценивается не только комфортность, но и внешний вид будущей постройки. Частный дом принято считать местом для отдыха, поэтому его стоит сделать красивым и комфортным. Если есть желание построить на приусадебном участке уникальную оранжерею, домик или беседку, то стоит попробовать подумать над возведением геодезического купола. С виду это довольно сложная конструкция, но построить ее способен даже не очень опытный строитель, а материальные затраты будут небольшими. В этой статье будет описано, как построить купол своими руками.

Определение геодезического купола

Специалисты считают, что большинство людей не имеют представления о такой конструкции здания, потому что она встречается очень редко. Именно поэтому стоит подробно описать все особенности и технические характеристики геодезического купола. Разработал постройки с несущей сетчатой оболочкой изобретатель Ричард Фуллер. Сначала он взял очень прочную конструкцию в виде сферы и разделил ее на небольшие треугольники, чьи стороны расположены на правильных геодезических линиях. Расчеты Ричарда Фуллера смогли сделать строительство купола простым и доступным любому человеку.

Изобретатель полагал, что подобная уникальная конструкция строения обязана была решить проблему быстрой постройки дешевого и комфортного дома. Эту разработку не оценили специалисты, и она не применяется в массовом строительстве. Однако для постройки уникального кафе или красивого летнего домика геодезический купол Фуллера является оптимальным вариантом.

Разработка Ричарда Фуллера является довольно устойчивой конструкцией. Геодезический купол равномерно распределяет всю массу, может выдержать огромные нагрузки и уменьшает финансовые вложения при строительстве фундамента. Уникальная сферическая форма способна противостоять самым мощным порывам ветра. Экономия при строительстве таких домов обусловлена сокращением общей площади боковой поверхности. В самом куполе круглые стены помогают качественной циркуляции воздуха, создавая комфортный микроклимат.

Главным недостатком можно считать очень сложные, по сравнению с простыми домами, математические расчеты. Так как конструкция состоит из огромного числа деталей, то необходимо утеплить довольно много стыков. Других существенных недостатков у геодезического купола нет.

Измерения и расчеты

При наличии желания построить геокупол своими руками сначала необходимо провести все математические расчеты. Главная задача расчета геодезического купола состоит в том, чтобы имея определенный радиус, получить такие данные:

• общую площадь и высоту строения;
• площадь поверхности геодезического купола;
• длину и число ребер;
• величину углов между ребрами строения;
• нужный тип и общее число специальных коннекторов.

Необходимо заострить внимание на таком узле для постройки геокупола, как специальный коннектор. Эта деталь представляет собой узел, соединяющий между собой все стропильные части. Так как коннектор является главным элементом для закрепления всей конструкции, то он изготавливается из прочного материала высокого качества.

В зависимости от конструкции геодезического купола и места расположения в нем, соединительный коннектор должен иметь разное количество лепестков. Все крепления для постройки купольного дома можно приобрести или изготовить своими руками. Хорошим примером может быть коннектор из обычной перфорированной ленты. Подобный коннектор обладает очень ценным качеством, потому что на нем довольно просто регулируется угол наклона. Геодезические купола с маленьким диаметром можно построить безконнекторным методом. Однако при строительстве большого дома применять для крепежа ребер коннектор из металла необходимо.

Для того чтобы произвести расчеты, нужно знать габариты строения. Необходимо запомнить, что общая площадь изготовленного геодезического купола будет немного меньше площади окружности, потому что в основании располагается многогранник, который вписан в круг. Высоту постройки можно определить по общей длине диаметра. Стоит заметить, что чем больше высота купола, тем конструкция будет больше похожа на сферу.

Чтобы рассчитать нужные детали будущей конструкции, стоит применить специальный онлайн-калькулятор. Нужно ввести данные о высоте и радиусе постройки, а калькулятор сделает расчеты геокупола и предоставит длину и число ребер, вид и количество соединительных коннекторов.

Строительство своими руками

Самыми подходящими для купольного строительства конструкциями можно считать небольшие теплицы, уютные беседки или дачные домики. Сначала необходимо выбрать место для постройки. Если это будет теплица, то нужно найти хорошо освещенный участок. Для домика или беседки подойдет немного затененная площадка. Участок под любое из этих строений выравнивается, а потом убирается на нем весь мусор и корни деревьев.

Теплица

Построить купольную теплицу легче всего. Чтобы ее собрать, не нужен фундамент, а материалом для основания могут быть обычные доски, бруски или металлические трубы. На предварительно подготовленной поверхности необходимо начать сборку основания теплицы-купола. В первую очередь собираются треугольники и скрепляются между собой. Для того чтобы не перепутать грани, их необходимо подписывать и сверяться с чертежом. Если теплица маленьких размеров, то при сборке соединительный коннектор стоит заменить простой монтажной лентой и крепежными материалами.

Изготовленный геодезический купол стоит накрыть простой пленкой. Намного лучше будет выглядеть купольная теплица, которая покрыта листами поликарбоната. Вырезанные из поликарбоната треугольники необходимо закрепить на каркасе, а все стыки закрыть декоративными рейками. С улицы геокупол можно украсить при помощи декоративного камня, посадить цветы и установить небольшой забор. Подобная купольная теплица будет уникальным украшением любого загородного дома.

Беседка

В виде геодезического купола можно построить беседку. Для этого необходимо придерживаться таких рекомендаций:

• наилучшим материалом для строительства такой беседки является профильная труба;
• концы подготовленных труб нужно сплющить или согнуть под углом в 12 градусов;
• на всех концах трубок стоит сделать отверстия;
• чтобы собрать детали конструкции, коннектор не нужен, необходимо просто соединить трубки при помощи болтов.

После изготовления конструкции купольной беседки следует не менее важный этап работ. Он заключается в накрытии круглой беседки с куполом. Материал для этого можно использовать самый разный. Если конструкция геодезического купола полностью не накрывается, и оставляется пара секций беседки открытыми, то их можно декорировать красивой тканью. В подобной комфортной беседке можно с удовольствием проводить свободное время с близкими и друзьями.

Купол способен стать основой уникального дома на дачном участке. Главным отличием от беседки и теплицы является необходимость строительства фундамента. Для того чтобы построить купольный дом, стоит придерживаться следующих рекомендаций:

• нужен хорошо теплоизолированный фундамент;
• к основанию фундамента крепятся специальные угловые стойки, которые укрепляются при помощи горизонтальных распорок;
• собирается конструкция купольного дома;
• снаружи дом необходимо обшить листами из фанеры.

Установив дверные и оконные рамы, стоит начать отделку геодезического дома изнутри. Во все проемы закладывается хороший утеплитель, который зашивается листами фанеры. Для того чтобы соорудить купольный дом, необходимо не более трех месяцев работы. Форма геодезического купола поможет сэкономить на количестве материалов.

При проживании в таком доме можно оценить основные преимущества этой конструкции:

• небольшая площадь потолка и стен сокращает потери тепла;
• округлые стены помогают воздуху хорошо циркулировать, создавая при этом комфортный микроклимат.

Купольное здание является оптимальным вариантом функционального, дешевого и уникального строения на территории дачного участка.

Источник

Как сделать складной купол для уличного бассейна

В данном обзоре мы расскажем, как своими руками сделать складной купол, который используется для накрытия уличного бассейна.

Самодельный складной купол предназначен для круглогодичного использования: защищает от солнца и предотвращает попадание мусора в бассейн.

Обратите внимание : в данном случае самодельный накрывной купол (его еще называют — павильон) используется для накрытия заглубленного бассейна.

Идеей изготовления складного купола для уличного бассейна с нами поделился автор YouTube канала «Сергей Сергей» — берите себе на заметку!

Возможно, вам также интересно будет прочитать статью-обзор: как сделать утепленную площадку под каркасный бассейн .

Пошаговый процесс изготовления складного купола для бассейна

• профильная труба (квадратная);
• листовой металл;
• ткань для пошива «чехла».

Установка закладных деталей

Первым делом вокруг бассейна автор выкопал ямки, в которые вставил и забетонировал круглые стальные трубы с закладными деталями (пластинами металла).

Изготовление дуг

Квадратную профильную трубу с помощью сварки автор нарастил до необходимой длины. С помощью трубогиба из профильной трубы были изготовлены дуги. В данном случае автору потребовалось 11 дуг.

В нижней части профильных труб автор сделал пропилы, которые нужны для крепления дуг к самодельным поворотным механизмам.

Подготовленные дуги необходимо зачистить болгаркой, после чего обработать грунтом с эмалью — двухслойное защитное покрытие значительно продлит срок их службы.

Сборка поворотного механизма

Для изготовления поворотного механизма мастер использовал детали, вырезанные из листового металла толщиной 6 мм.

Для крепления металлического каркаса складного купола потребуется два поворотных механизма, которые расположены по краям бассейна напротив друг друга.

Сборка металлического каркаса и крепление «чехла»

Собранные поворотные механизмы крепятся к закладным деталям.

После этого к поворотным механизмам (для этого в них предусмотрены отверстия) крепятся концы дуг из профильной трубы.

На последнем этапе останется только сшить из ткани «чехол», и натягиваем его на металлический каркас.

Обратите внимание

Обязательно учитывайте тот момент, что диаметр накрывного купола должен быть примерно на 40-50 см больше диаметра самого бассейна!

Вместо стальной профильной трубы можно использовать алюминиевый профиль — тогда металлоконструкция получится легче.

Чтобы легче было открывать и закрывать купол, можно использовать ручную или электрическую лебедку.

Видео по теме:

Источник

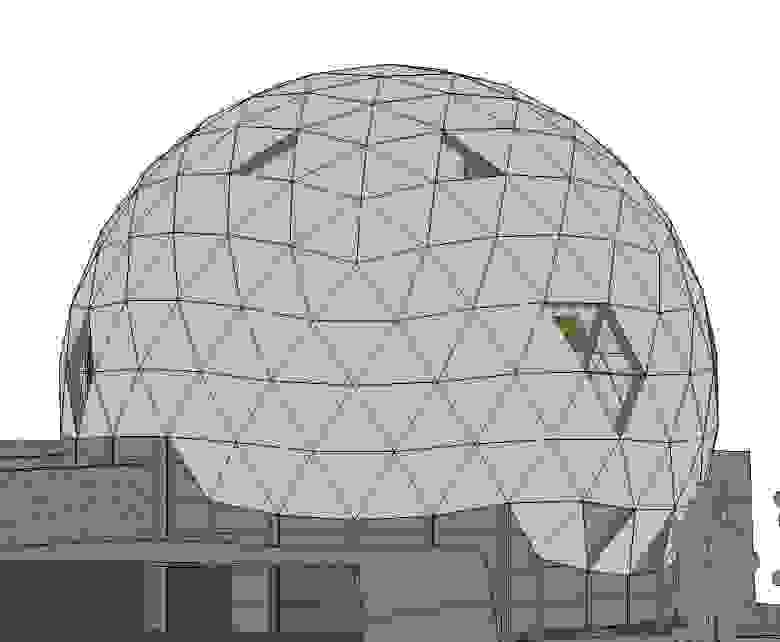
Геодезический купол. Об устройстве и моем опыте расчетов

Пожалуй сложно назвать геодезические купола чем-то необычным или новым. В этой заметке я расскажу немного об этих конструкциях в общем, об их устройстве, а также покажу на примере как я кое что на эту тему считал. Код тоже будет.

Википедию цитировать не буду. Почему я выбрал купол в качестве дома?

• При равном объеме площадь поверхности сферы будет меньше, чем у любой другой формы. Это положительно влияет как на материалоемкость, так и на энергозатраты при эксплуатации.
• Мне нравится как выглядит сфера.
• Это интересный инженерный проект, в каком-то смысле даже вызов. Это сложно, трудно и потому весело!

Как это геодезические сферы устроены вообще? С первого взгляда кажется, что это какое-то переплетение рёбер и уловить систему сложно. В этой заметке попробуем разобраться.

В основе таких конструкций лежит икосаэдр или октаэдр. В общем правильный многогранник.
В моем случае это был именно икосаэдр и чаще используют его. Далее берем одну грань и заменяем ее на несколько треугольников, вершины которых лежат на сфере, центр которой совпадает с центром икосаэдра. Звучит не слишком складно. Отвлечемся.

Есть замечательный калькулятор www.acidome.ru который позволяет в реальном времени покрутить геодезик. Берем в качестве основы icosahedron, ставим частоту 1, часть сферы 1/1.

Это и есть наш основной икосаэдр. Частота это на сколько частей мы разобьем каждое ребро икосаэдра. Ставим 3,4, 5 и ничего становится непонятно. Переключаем в режим кровли и ищем пятиугольники. В тех местах, где у нас вершина икосаэдра — будет пятиугольник. Между тремя пятиугольниками грань икосаэдра.

Если внимательно смотреть на геодезик и знать, что искать (обычно пятиугольник), то становится видна регулярность структуры. На Биосфере в Монреале при должном усердии можно найти пятиугольники и посчитать частоту. Частота у нас равна количеству ребер между двумя пятиугольниками.

Сами “большие” треугольники, с вершинами на вершинах икосаэдра также имеют структуру. На acidome в режиме кровли это видно по цвету. Треугольники расположены симметрично относительно центра “большого” треугольника. Количество их типов меньше общего числа треугольников. В случае с частотой 5 уникальных треугольников 9.

В процессе проектирования дома я столкнулся с задачей постройки сферы в Dynamo. Это такой инструмент, который позволяет научить Autodesk Revit работать со сложными формами. Такая среда визуального программирования.
Погуглив я даже нашел скетч, который в Dynamo строил геодезическую сферу. Сферу то он строил, да не ту.

Дело вот в чем. Когда мы берем одно ребро икосаэдра и делим его на мелкие треугольники — сделать это можно несколькими способами. В acidome за это отвечает переключатель “метод разбиения”.

Найденный скетч строил сферу методом равных хорд. Что это значит? Мы берем большой треугольник икосаэдра, каждое его ребро делим на нужное нам количество частей, соединяем точки на ребрах между собой и получаем плоскую сетку из треугольников. Затем эту сетку мы проецируем на сферу. Все бы хорошо, но сами эти треугольники достаточно сильно отличаются по размеру. Центральный больше всех. Оно и понятно, центр “большого” треугольника у нас на максимальном расстоянии от сферы. Это плохо, так как в этом случае сложнее оптимизировать расход материалов. Будет больше отходов.

Другой метод разбиения (равными дугами) предполагает, что мы строим поверх “большого” треугольника дуги и уже их делим на равные части. Подход отличается, простой проекцией не обойтись.

Скетч не подходил. Я попытался его исправить и в итоге мне пришлось нырнуть в это дело с головой.

Как оказалось помимо визуальной среды Dynamo имеет встроенный Python. С этим языком я ранее не сталкивался, но где наша не пропадала? В конце концов это просто инструмент.

Дальше будут кусочки кода, прошу обратить внимание, что это мой hello world в python, а целью было не построить максимально эффективное и производительное решение, а построить нужную сферу.

Метод равных дуг.

Берем одну из граней икосаэдра и из углов этого треугольника строим дуги.

Затем дуги делим на равные части и соединяем точки на дугах новыми дугами. У всех дуг один центр — центр сферы. Точки соединяем не все со всеми, а одноименные. На картинке оно выглядит попроще, чем в коде.

Опа, а дуги то не пересекаются! Не слишком беглое гугление вывело меня на книгу, которая подтвердила мои предположения о том, что нужно в качестве вершины ребра геодезика использовать центр треугольника, образованного пересечением дуг. Также курил исходники acidome, но не помню нашел ли там этому подтверждение. Помню, что было интересно.
Центры надо как-то найти. Это центр треугольника и это не сложно, но нужно было понять где же у нас в ворохе точек эти треугольники. Мне показалось самым простым вариантом соединять ближайшие друг к другу точки.

Теперь нам нужно соединить между собой собранные на разных этапах точки, которые и являются вершинами ребер геодезической сферы. На картинке эти точки видно хорошо, но вот когда они в массиве — все сложнее. Было несколько вариантов, но так как задача была с наименьшими трудозатратами получить рабочий скрипт, вышло вот это:

Сегмент готов. Наверное существует какой-то правильный путь для решения этой задачи, но я проложил свой.

Дальше сегмент разворачивается, несколько раз копируется копируется и получается полная сфера. Вот один из поворотов:

Скриптик вышел страшненький, я его пару раз переписывал, так как были проблемы с экспортом в Revit. Думал, что проблемы с построением. В итоге на форуме Dynamo индус подсказал украинцу и все удалось!

Теперь можно строить сферу любой частоты и любого диаметра. Сравнение размеров с результатами acidome показало, что все сходится с высокой точностью. Повторяемость это хорошо.

Также я занялся оптимизацией размеров с целью минимизации обрезков. Так как все размеры были у меня на руках это было не так трудно. В итоге радиус сферы получился 5,65 метров при частоте 5. Такие размеры позволяют мне достаточно эффективно использовать материалы шириной 125 см. Такую ширину имеют листы OSB, листового металла, утеплителя, гипсокартона. При хорошей оптимизации количество обрезков минимально. Наилучших результатов можно добиться путем расчета раскладок треугольников на материале, но этим я не занимался.

Дальше было проще, так как Revit съел сложную форму и позволил с ней работать примерно с тем же успехом, что и с квадратно-параллельной.

Конечно, трудности на этом не закончились, но это уже совсем другая история.

Источник