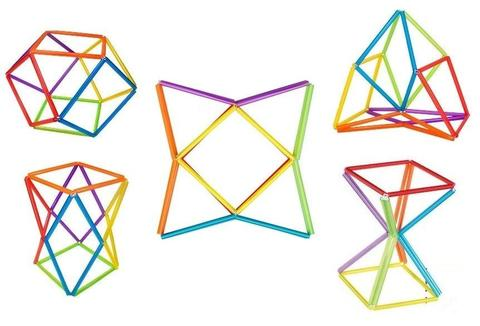
Красивые многогранники своими руками

Сообщество людей готовых на бескорыстной основе разыгрывать игры и программы размещённые на сервисе Steam.

Розыгрыши проводятся через steamgifts.

Сайты одобренные нашим сообществом:

https://www.steamgifts.com — проведение и участие в розыгрышах. (наш герой)

https://www.sgtools.info — доп. инструментарий для steamgifts.

Пикабу в мессенджерах

Активные сообщества

Тенденции

Ромботриаконтаэдр из картона

Представляю Вам новую свою схему и видеоинструкцию по сборке одного из Каталановых тел* — ромботриаконтаэдра. Но для начала немного описания многогранника.

Ромботриаконтаэдр — это выпуклый тридцатигранник с одинаковыми ромбическими гранями. Он состоит из 30 граней (золотых ромбов**), 32 вершин и 60 рёбер. Является двойственным по отношению к икосододекаэдру.

*Каталановы тела — это выпуклые многогранники, обладающие двумя свойствами:

1. Все грани одинаковые, но не являются правильными многоугольниками;

2. Многогранник относится к одному из трёх существующих типов пространственной симметрии.

Эти многогранники названы в честь бельгийского математика Эжена Каталана, который впервые описал их в 1865 году.

**Золотой ромб — это ромб, чьи диагонали относятся друг к другу как φ (золотое сечение, равное примерно 1,618).

Использование ромботриаконтаэдра в мире:

Тридцатигранные игральные кости.

Игрушка Ball of Whacks от Роджера фон Эйк.

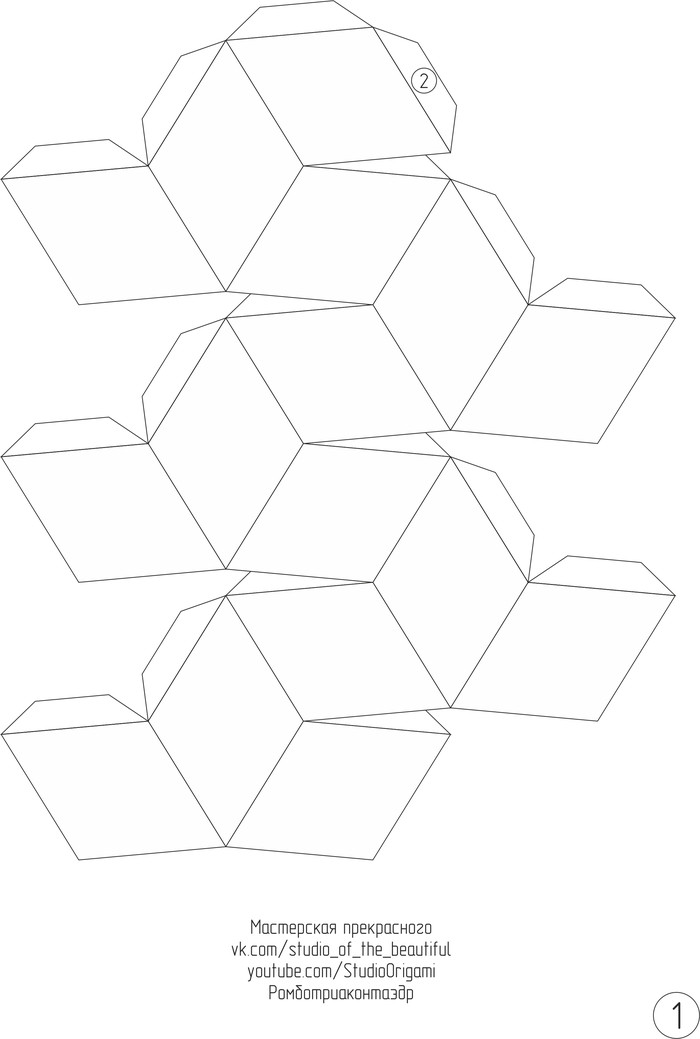
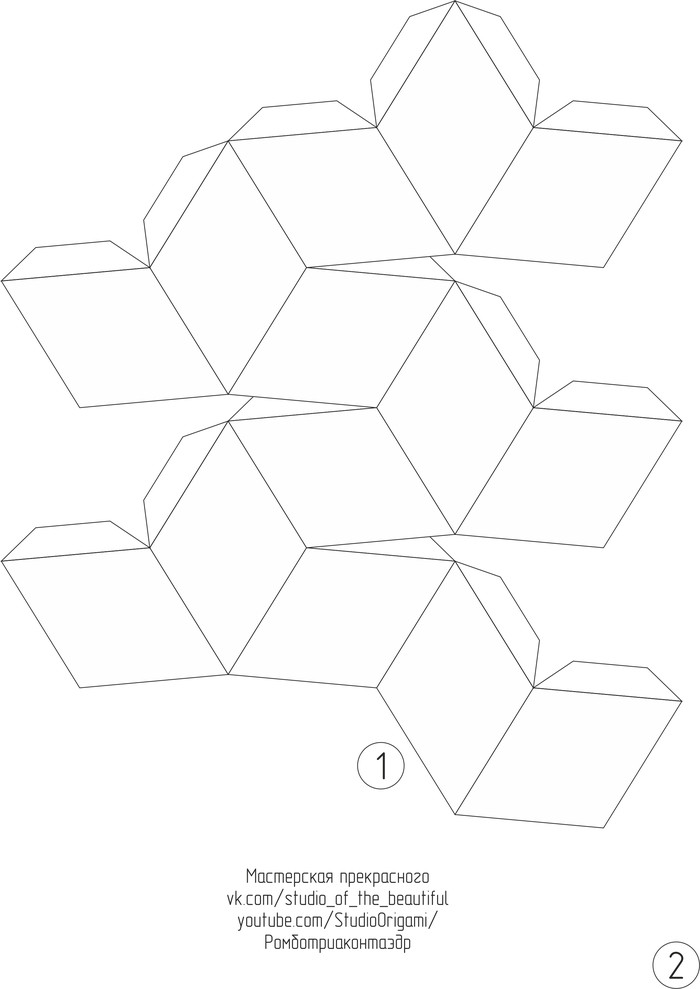
А теперь сама инструкция для сборки. Для развёртки ромботриаконтаэдра необходимо 2 листа цветного картона формата А4. Длина ребра у многогранника — 3,8 см, а высота многогранника — 10,5 см. Развёртка ромботриаконтаэдра в формате pdf или изображениями ниже:

Ниже представлена видеоинструкция по сборке ромботриаконтаэдра:

Также смотрите предыдущие мои посты про многогранники:

Многогранник Икосаэдр из бумаги. Kusudama by Mitsunobu Sonobe

Многогранник Икосаэдр — замечательная и интересная оригами поделка из бумаги, которая станет подарком для ценящих людей. Такой многогранник — кусудаму можно использовать как елочное украшение на Новый год в качестве игрушки. Для создания многогранника понадобиться 30 квадратных листов бумаги. Размер одного листа 8*8 см. Designed by: Mitsunobu Sonobe

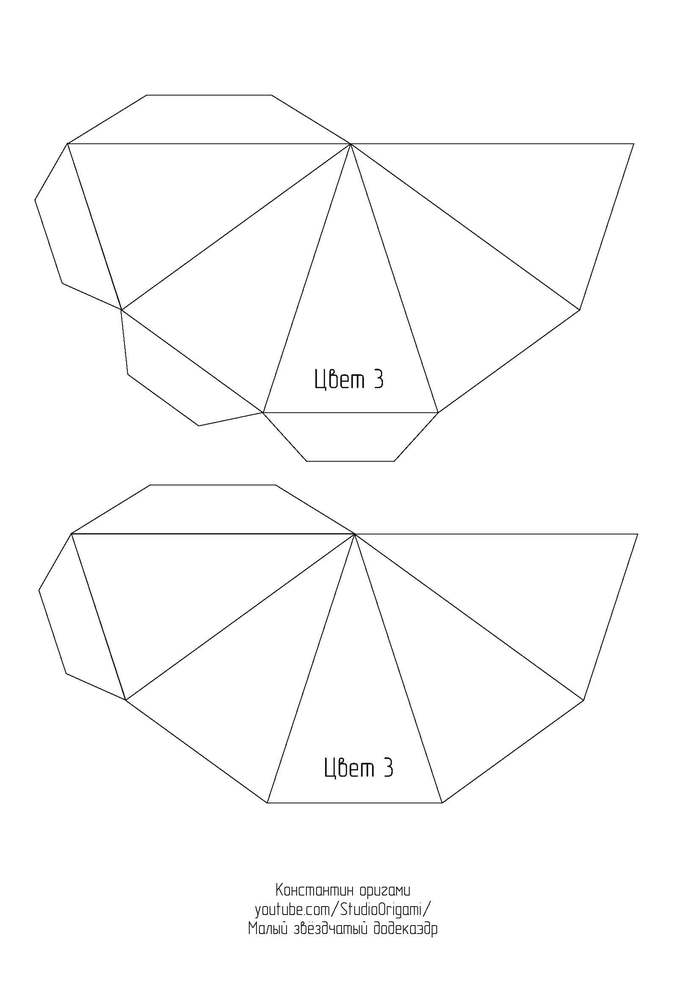
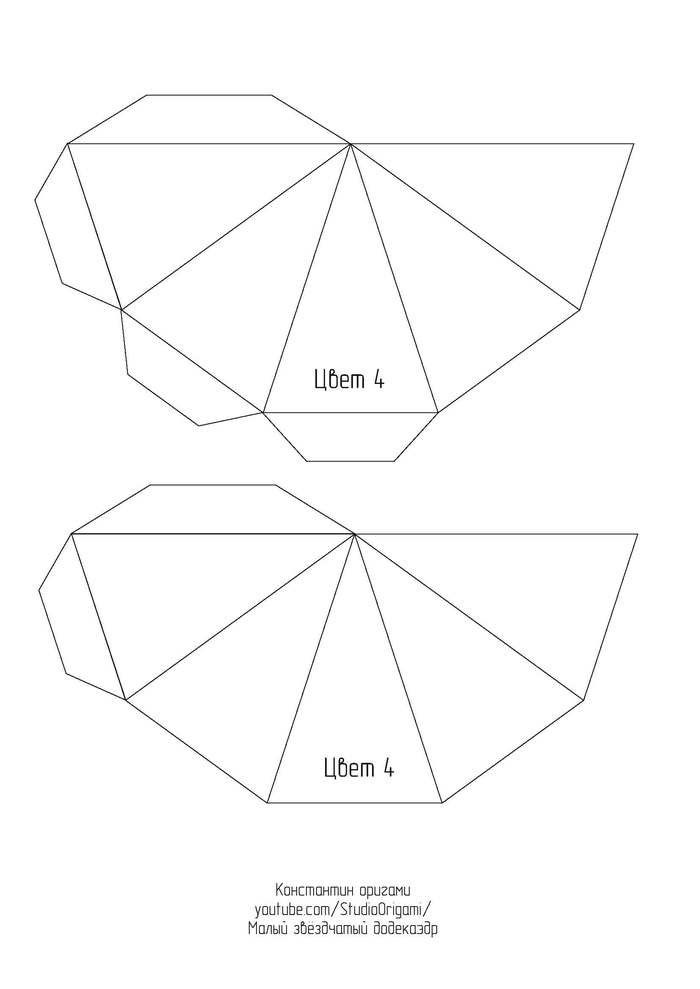
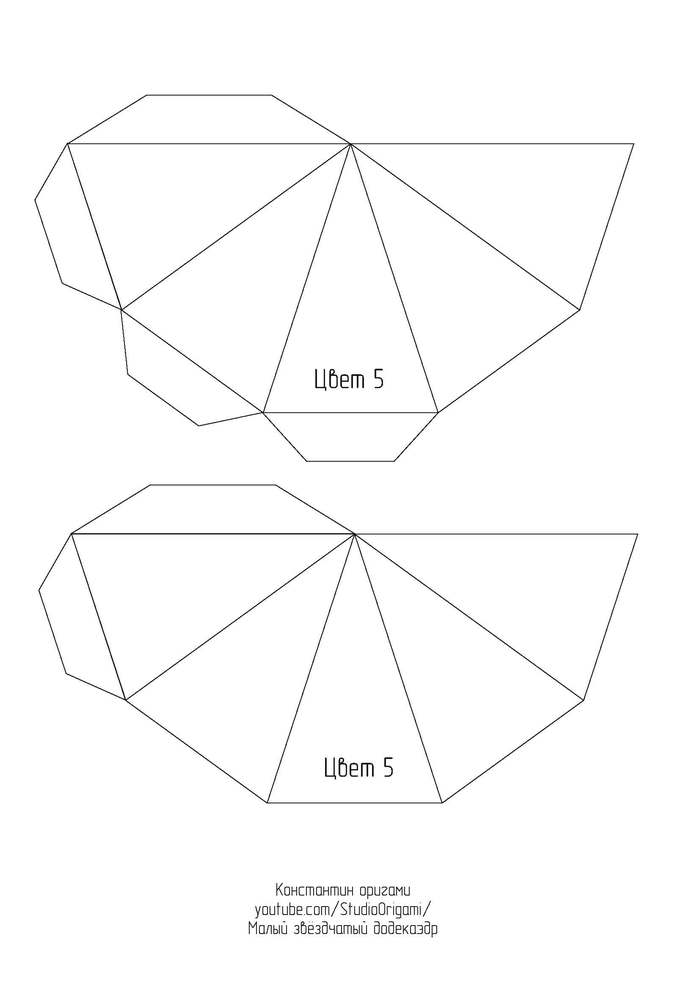
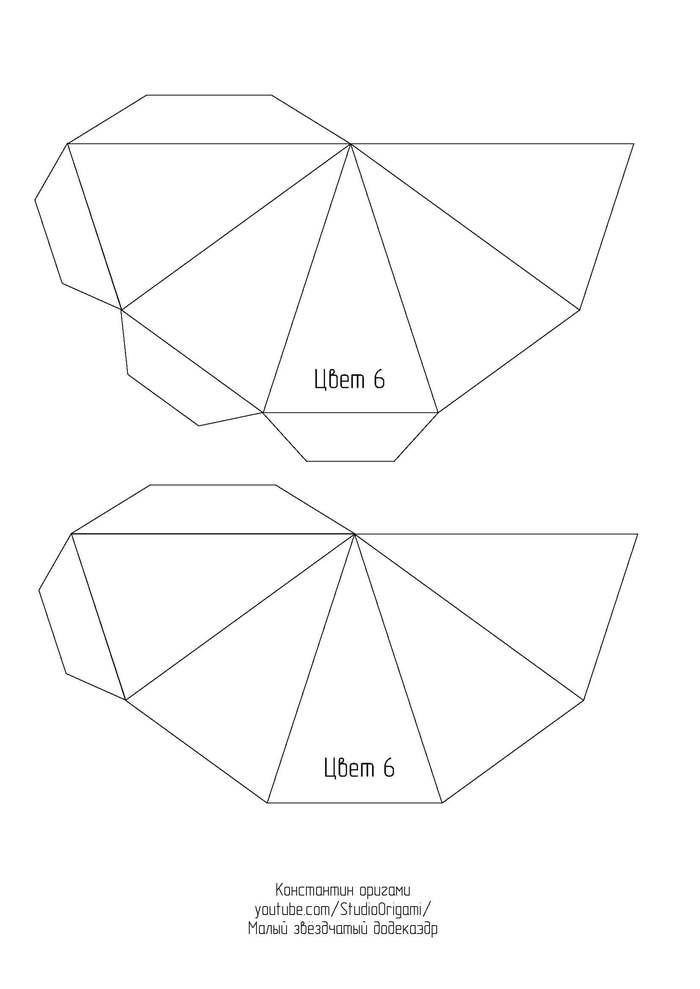
Малый звёздчатый додекаэдр из картона.

Представляю Вам новую свою схему и видеоинструкцию по сборке одного из тел Кеплера-Пуансо* — малого звёздчатого додекаэдра.

Малый звёздчатый додекаэдр является одним из четырёх невыпуклых правильных многогранников. Он состоит из 12 граней в виде пентаграмм с пятью пентаграммами, сходящимися в каждой вершине. Он имеет то же самое расположение вершин, что и выпуклый правильный икосаэдр. Кроме того, у него то же самое расположение рёбер, что и у большого икосаэдра. Этот многогранник считается первой звёздчатой формой додекаэдра.

*Тело Кеплера-Пуансо — это тело, представляющее собой правильный звёздчатый многогранник, не являющийся соединением платоновых и звёздчатых тел.

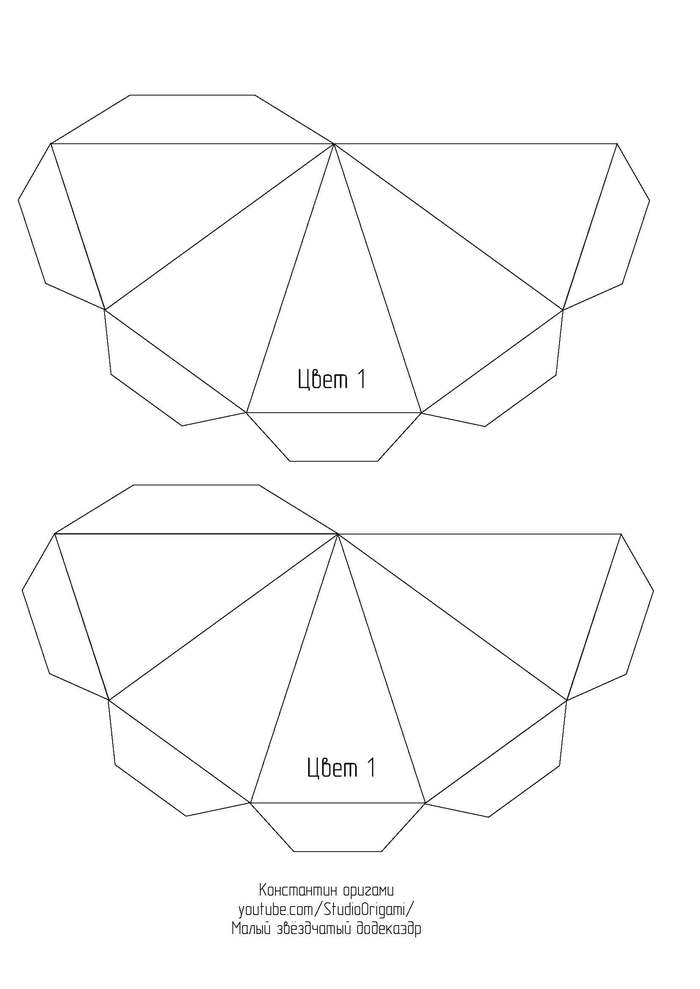
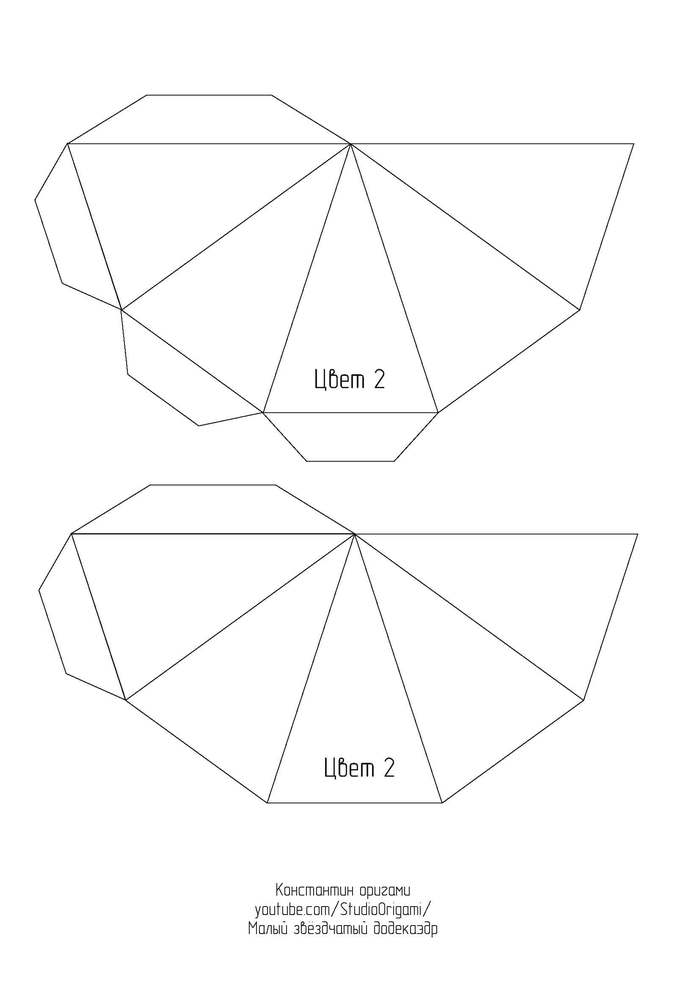
Для развёртки малого звёздчатого додекаэдра необходимо 6 листов цветного картона формата А4. Длина ребра получается 8 см, а высота многогранника — около 25 см. Ссылка на развёртку в формате pdf или картинками ниже:

Также смотрите видеоинструкцию по сборке многогранника:

Если понравилось, то смотрите предыдущие мои посты про многогранники:

Как сделать ромбододекаэдр

Ромбододекаэдр (Rhombic Dodecahedron) — это двенадцатигранник, составленный из одинаковых ромбов. У ромбододекаэдра 14 вершин и 24 ребра. Ромбододекаэдр является каталановым многогранником. Двойственным многогранником ромбододекаэдра является кубооктаэдр.

Каталановы многогранники — это выпуклые многогранники, обладающие двумя свойствами:

1. Все грани одинаковые, но не являются правильными многоугольниками;

2. Многогранник относится к одному из трёх существующих типов пространственной симметрии (тетраэдрический, октаэдрический или икосаэдрический).

Где встречается ромбододекаэдр:

Головоломка наподобие кубика Рубика.

Капелла Гранато в долине Циллерталь (Австрия).

А теперь сама инструкция для сборки. Для развёртки ромбододекаэдра необходимо 2 листа двухстороннего цветного картона формата А4 (или плотной бумаги). Длина ребра у ромбододекаэдра — 6,1 см. Развёртку многогранника в формате pdf вы можете скачать по ссылке. Если у Вас нет принтера, то Вы можете сами нарисовать развёртку ромбододекаэдра с помощью линейки и карандаша, смотря видеоинструкцию ниже:

Кубооктаэдр из картона

Представляю Вам новую свою схему и видеоинструкцию по сборке одного из Архимедовых тел* — кубооктаэдра. Но в начале, как обычно, немного описания многогранника.

Кубооктаэдр (кубоктаэдр) — это полуправильный многогранник, состоящий из 14 граней (8 правильных треугольников и 6 квадратов). В кубооктаэдре 12 одинаковых вершин, в которых сходятся два треугольника и два квадрата, а также 24 одинаковых ребра, каждое из которых разделяет треугольник и квадрат. Двойственный к кубооктаэдру многогранник — ромбододекаэдр.

*Архимедовы тела — это выпуклые многогранники, обладающие двумя свойствами:

1. Все грани являются правильными многоугольниками двух или более типов;

2. Многогранник относится к одному из трёх существующих типов пространственной симметрии.

Использование кубооктаэдра в мире:

Головоломка наподобие кубика Рубика.

Игрушка Geo Twister.

Памятники в Императорском дворе Шугакуин (Япония)

Весак Куду — традиционные фонари, которые ежегодно делают на Шри-Ланке в честь праздника Весак, обычно имеют кубооктаэдрическую форму.

Четырнадцатигранные игральные кости.

Кубооктаэдр даже засветился в Звёздном Пути (оригинальный сериал — сезон 2, серия 22).

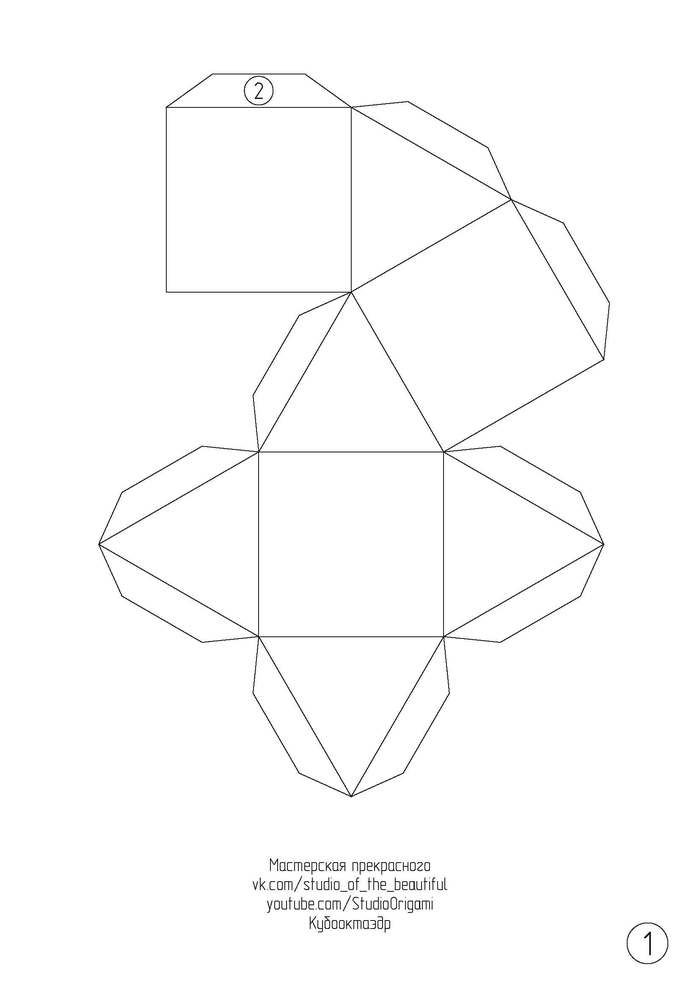
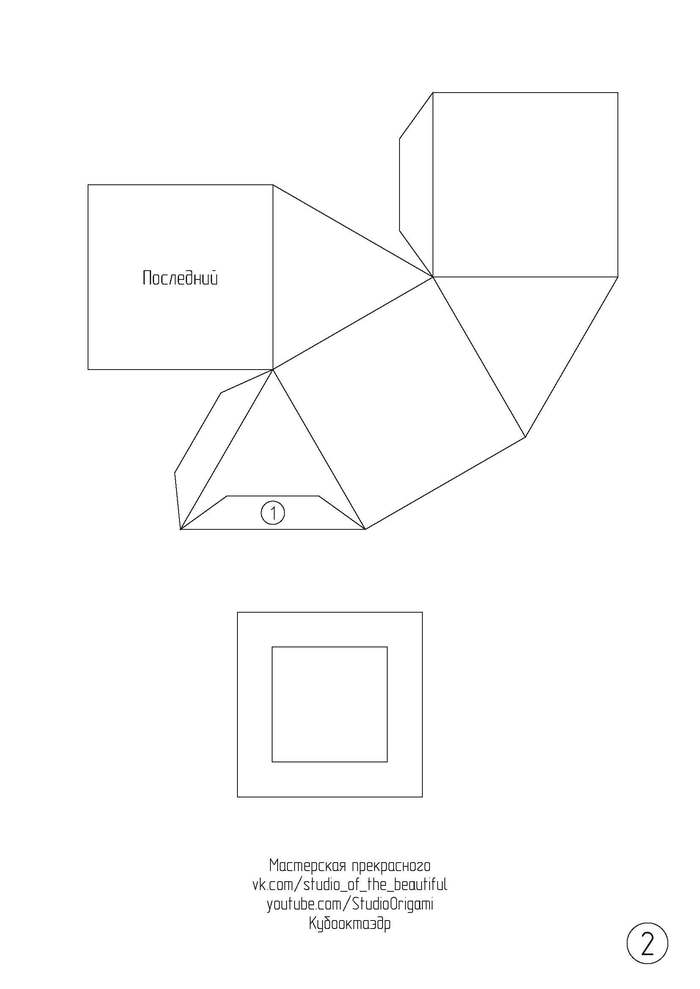
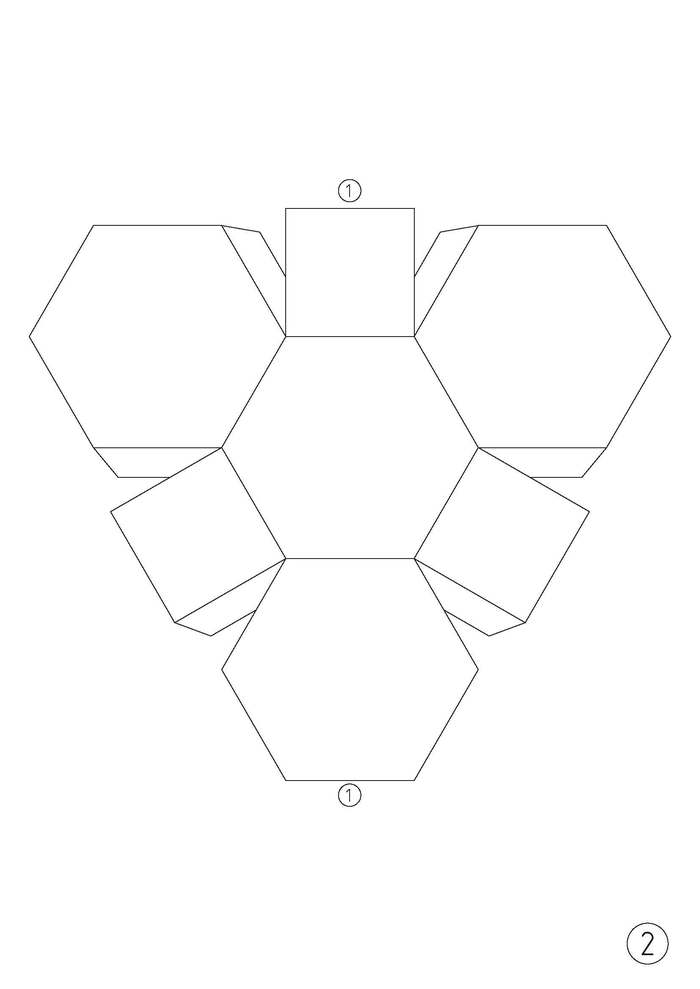
А теперь сама инструкция для сборки. Для развёртки кубооктаэдра необходимо 2 листа цветного картона формата А4 (или плотной бумаги). Длина ребра у многогранника — 5,4 см, а высота многогранника — 7,5 см. Развёртка кубооктаэдра в формате pdf или изображениями ниже:

Ниже представлена видеоинструкция по сборке кубооктаэдра:

Также смотрите мой предыдущий мои пост про многогранники из картона:

Усечённый октаэдр из картона.

Представляю Вам свою схему и видеоинструкцию по сборке одного из Архимедовых тел — усечённого октаэдра.

Усечённый октаэдр — полуправильный многогранник, состоящий из 14 граней (8 правильных шестиугольников и 6 квадратов). В усечённом октаэдре 24 одинаковых вершины, в каждой из которых сходятся два шестиугольника и квадрат, а также 24 ребра, каждое из которых разделяет шестиугольник и квадрат, и 12 рёбер, каждое из которых разделяет два шестиугольника.

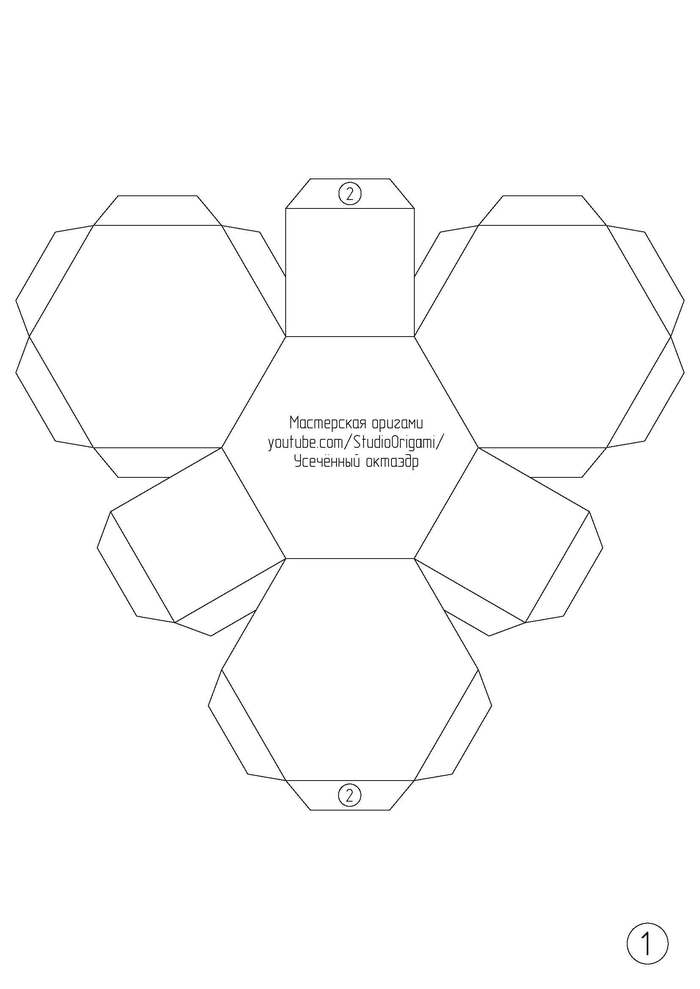
Для развёртки усечённого октаэдра необходимо 2 листа цветного картона формата А4. Сама развёртка многогранника представлена в виде картинки ниже, или по ссылке в формате pdf.

Если Вам что-то непонятно при сборке многогранника, то можете посмотреть мою видеоинструкцию:

Ещё можете посмотреть мои видеоинструкции про другие многогранники:

Как сделать октаэдр

Октаэдр (квадратная бипирамида, восьмигранник) — многогранник, гранями которого являются восемь правильных треугольника. Октаэдр является одним из пяти правильных многогранников (Платоновы тела). У октаэдра 8 граней, 6 вершины и 12 рёбер. Двойственным многогранником октаэдра является гексаэдр (куб).

Правильный многогранник — это выпуклый многогранник, состоящий из одинаковых правильных многоугольников и обладающий одной из пространственной симметрией. У октаэдра октаэдрическая симметрия.

Где встречается октаэдр:

Головоломка Октаэдр Трайбера

Восьмигранные игральные кости.

Игра Octahedron от Demimonde.

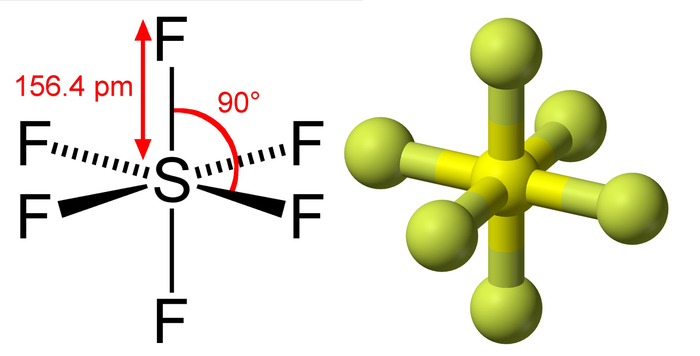
Молекулярная структура Фторида серы(VI).

Террариум для растений.

Монолит Мортиса из Звёздных Войн: Войны Клонов (3 сезон, 15 серия).

Корабль королевы Борг из Звёздного Пути: Вояджер (5 сезон 15/16 серия)

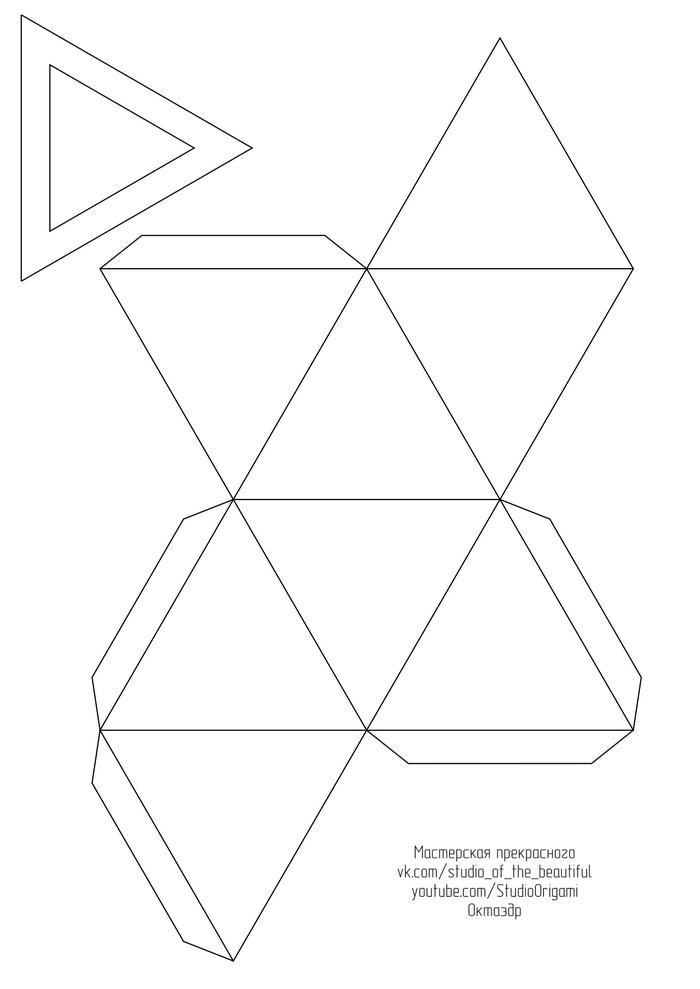
А теперь сама инструкция для сборки. Для развёртки октаэдра необходим лист двухстороннего цветного картона формата А4. Длина ребра у октаэдра получается 8 см. Развёртку октаэдра в формате pdf Вы можете скачать по ссылке или картинкой ниже:

Если у Вас нет принтера, то Вы можете сами нарисовать развёртку октаэдра с помощью линейки и циркуля, смотря видеоинструкцию ниже:

Усечённый тетраэдр из картона

Представляю Вам новую свою схему и видеоинструкцию по сборке одного из Архимедовых тел* — усечённого тетраэдра.

Усеченный тетраэдр — это выпуклый многогранник, состоящий из 8 граней (4 правильных шестиугольников и 4 равносторонних треугольников), 12 вершин и 18 рёбер. Его можно построить, обрезав все 4 вершины правильного тетраэдра на треть от первоначальной длины ребра.

*Архимедовы тела — это выпуклые многогранники, обладающие двумя свойствами:

1. Все грани являются правильными многоугольниками двух или более типов;

2. Многогранник относится к одному из трёх существующих типов пространственной симметрии (для усечённого тетраэдра двойственным многогранником является триакистетраэдр).

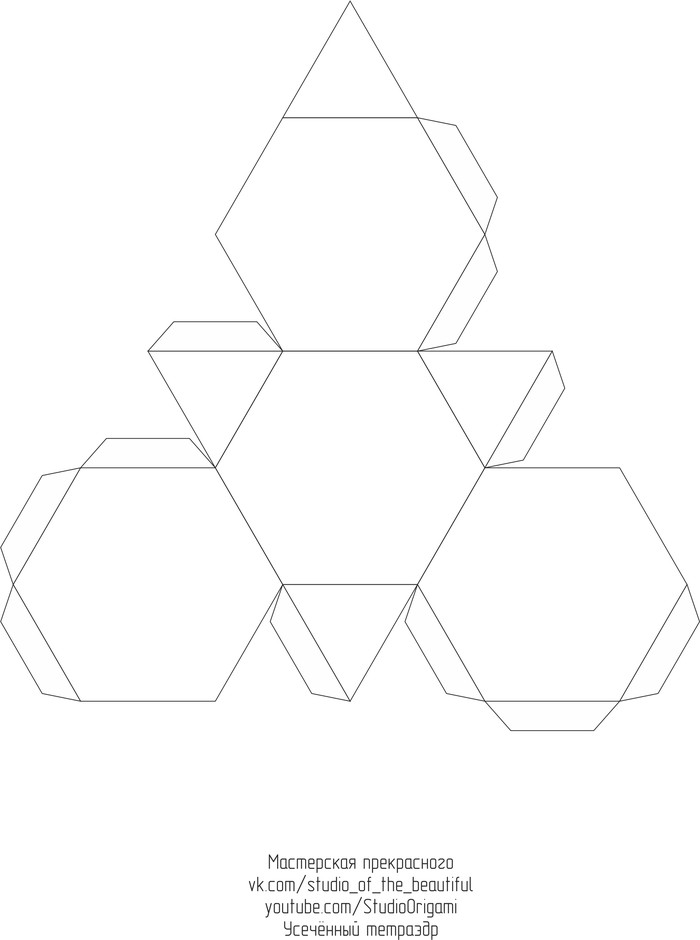
Для развёртки усечённого тетраэдра необходим 1 лист цветного картона формата А4. Длина ребра у многогранника — 3,5 см, а высота многогранника — 5 см. Развертка усечённого тетраэдра в формате pdf или изображением ниже:

Смотрите видеоинструкцию по сборке усечённого тетраэдра:

Если понравилось, то смотрите предыдущие мои посты про многогранники:

Как сделать квадратную пирамиду

Представляю видеоинструкцию по сборке квадратной пирамиды.

Квадратная пирамида — это пирамида, имеющая квадратное основание. Квадратная пирамида состоит из 5 граней (4 треугольников и 1 квадрата), 5 вершин, 8 рёбер.

Пирамида — это многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. Данная пирамида также является одним из тел Джонсона. Тело Джонсона (правильногранный многогранник) — это выпуклый многогранник, каждая грань которого является правильным многоугольником, при этом многогранник не должен является ни платоновым телом, ни архимедовым, ни призмой, ни антипризмой.

Квадратная пирамида много где встречается в мире:

Источник