Колебательный контур 50гц своими руками

Параллельный колебательный контур

В прошлой статье мы с вами рассмотрели последовательный колебательный контур, так как все участвующие в нем радиоэлементы соединялись последовательно. В этой же статье мы рассмотрим параллельный колебательный контур, в котором катушка и конденсатор соединяются параллельно.

Параллельный колебательный контур

Идеальный колебательный контур

На схеме идеальный колебательный контур выглядит вот так:

L – индуктивность, Генри

С – емкость, Фарад

Реальный колебательный контур

В реальности у нас катушка обладает приличным сопротивлением потерь, так как намотана из провода, да и конденсатор тоже имеет некоторое сопротивление потерь. Потери в емкости очень малы и ими обычно пренебрегают. Поэтому оставим только одно сопротивление потерь катушки R. Тогда схема реального колебательного контура примет вот такой вид:

R – это сопротивление потерь контура, Ом

L – индуктивность, Генри

С – емкость, Фарад

Принцип работы параллельного колебательного контура

Давайте подцепим к генератору частоты реальный параллельный колебательный контур

Что будет, если мы подадим на контур ток с частотой в ноль Герц, то есть постоянный ток? Он спокойно побежит через катушку и будет ограничиваться лишь сопротивлением потерь R самой катушки. Через конденсатор ток не побежит, потому что конденсатор не пропускает постоянный ток. Об это я писал еще в статье конденсатор в цепи постоянного и переменного тока.

Давайте тогда будем добавлять частоту. Итак, с увеличением частоты у нас конденсатор и катушка начнут оказывать реактивное сопротивление электрическому току.

Реактивное сопротивление катушки выражается по формуле

а конденсатора по формуле

Более подробно про это можно прочитать в этой статье.

Если плавно увеличивать частоту, то можно понять из формул, что в самом начале при плавном увеличении частоты конденсатор будет оказывать бОльшее сопротивление, чем катушка индуктивности. На какой-то частоте реактивные сопротивления катушки X_L и конденсатора X_C уравняются. Если далее увеличивать частоту, то уже катушка уже будет оказывать большее сопротивление, чем конденсатор.

Резонанс параллельного колебательного контура

Очень интересное свойство параллельного колебательного контура заключается в том, что при Х_L = Х_С у нас колебательный контур войдет в резонанс. При резонансе колебательный контур начнет оказывать большее сопротивление переменному электрическому току. Еще часто это сопротивление называют резонансным сопротивлением контура и оно выражается формулой:

R_рез – это сопротивление контура на резонансной частоте

L – собственно сама индуктивность катушки

C – собственно сама емкость конденсатора

R – сопротивление потерь катушки

Формула резонанса

Для параллельного колебательного контура также работает формула Томсона для резонансной частоты как и для последовательного колебательного контура:

F – это резонансная частота контура, Герцы

L – индуктивность катушки, Генри

С – емкость конденсатора, Фарады

Как найти резонанс параллельного колебательного контура на практике

Ладно, ближе к делу. Берем паяльник в руки и спаиваем катушку и конденсатор параллельно. Катушка на 22 мкГн, а конденсатор на 1000пФ.

Итак, реальная схема этого контура будет вот такая:

Для того, чтобы все показать наглядно и понятно, давайте добавим к контуру последовательно резистор на 1 КОм и соберем вот такую схему:

На генераторе мы будет менять частоту, а с клемм X1 и X2 мы будем снимать напряжение и смотреть его на осциллографе.

Нетрудно догадаться, что у нас сопротивление параллельного колебательного контура будет зависеть от частоты генератора, так как в этом колебательном контуре мы видим два радиоэлемента, чьи реактивные сопротивления напрямую зависит от частоты, поэтому заменим колебательный контур эквивалентным сопротивлением контура R_кон.

Упрощенная схема будет выглядеть вот так:

Интересно, на что похожа эта схема? Не на делитель ли напряжения? Именно! Итак, вспоминаем правило делителя напряжения: на меньшем сопротивлении падает меньшее напряжение, на бОльшем сопротивлении падает бОльшее напряжение. Какой вывод можно сделать применительно к нашему колебательному контуру? Да все просто: на резонансной частоте сопротивление R_кон будет максимальным, вследствие чего у нас на этом сопротивлении “упадет” бОльшее напряжение.

Начинаем наш опыт. Поднимаем частоту на генераторе, начиная с самых маленьких частот.

Как вы видите, на колебательном контуре “падает” малое напряжение, значит, по правилу делителя напряжения, можно сказать, что сейчас у контура малое сопротивление R_кон

Добавляем частоту. 11,4 Килогерца

Как вы видите, напряжение на контуре поднялось. Это значит, что сопротивление колебательного контура увеличилось.

Добавляем еще частоту. 50 Килогерц

Заметьте, напряжение на контуре повысилось еще больше. Значит его сопротивление еще больше увеличилось.

Обратите внимание на цену деления одного квадратика по вертикали, по сравнению с прошлым опытом. Там было 20мВ на один квадратик, а сейчас уже 500 мВ на один квадратик. Напряжение выросло, так как сопротивление колебательного контура стало еще больше.

И вот я поймал такую частоту, на которой получилось максимальное напряжение на колебательном контуре. Обратите внимание на цену деления по вертикали. Она равняется двум Вольтам.

Дальнейшее увеличение частоты приводит к тому, что напряжение начинает падать:

Снова добавляем частоту и видим, что напряжение стало еще меньше:

Что происходит на резонансной частоте в параллельном колебательном контуре

Давайте более подробно рассмотрим эту осциллограмму, когда у нас было максимальное напряжение с контура.

Что здесь у нас произошло?

Так как на этой частоте был всплеск напряжения, следовательно, на этой частоте параллельный колебательный контур имел самое высокое сопротивление R_кон. На этой частоте Х_L = Х_С. Потом с ростом частоты сопротивление контура снова упало. Это и есть то самое резонансное сопротивление контура, которое выражается формулой:

Резонанс токов

Итак, давайте допустим, мы вогнали наш колебательный контур в резонанс:

Чему будет равняться резонансный ток I_рез ? Считаем по закону Ома:

Но самый прикол в том, что у нас при резонансе в контуре появляется свой собственный контурный ток I_кон , который не выходит за пределы контура и остается только в самом контуре! Так как с математикой у меня туго, поэтому я не буду приводить различные математические выкладки с производными и комплексными числами и объяснять откуда берется контурный ток при резонансе. Именно поэтому резонанс параллельного колебательного контура называется резонансом токов.

Добротность параллельного колебательного контура

Кстати, этот контурный ток будет намного больше, чем ток, который проходит через контур. И знаете во сколько раз? Правильно, в Q раз. Q – это и есть добротность! В параллельном колебательном контуре она показывает во сколько раз сила тока в контуре I_кон больше сила тока в общей цепи I_рез

Если сюда еще прилепить сопротивление потерь, то формула примет вот такой вид:

R – сопротивление потерь на катушке, Ом

Применение параллельного колебательного контура

Параллельный колебательный контур применяется в радиоприемном оборудовании, где надо выделить частоту какой-либо станции. Также с помощью колебательного контура можно построить различные резонансные фильтры.

Источник

Резонансный трансформатор Тесла — больше не секрет

Знакомство с трансформатором Н. Тесла.

Новомодный феномен резонансного трансформатора Николы Тесла возник не давно, а Интернет забит фотографиями и интригующими видеосъемками молний и коронарных разрядов.

Вспомним, что трансформатор первоначально был предназначен не для показательного выступления в цирке, а для передачи радиосигналов на далекие расстояния. В связи с этим предлагаю ознакомиться с его принципом работы и найти ему практическое применение.

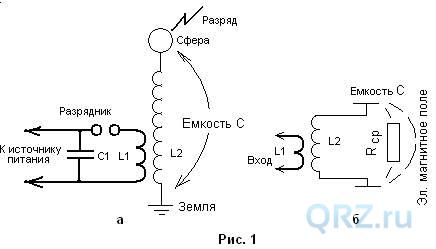
Трансформатор Тесла состоит из двух основных частей, см. рис.1а;

1. Генерирующей части, состоящей из высоковольтного источника питания, накопительного конденсатора С1, разрядника и катушки связи L1. Частота генерации зависит от напряжения питания, емкости конденсатора С1, характеризующее время разряда, а так же промежутком между электродами разрядника;

2. Резонансной катушки индуктивности L2, заземления и сферы, см. рис. 1а.

Если вглядеться в схему этого трансформатора внимательнее, то мы увидим известную схему последовательного колебательного контура, состоящего из катушки индуктивности L2 с открытой емкостью С, образованной между сферой и землей. Это открытый колебательный контур, который был открыт Дж. К. Максвеллом.

Обратимся к классической теории принципа действия открытого колебательного контура:

Как известно колебательный контур состоит из катушки индуктивности и конденсатора. Исследуем простейший колебательный контур, катушка которого состоит из одного витка, а конденсатор представляет собой две рядом расположенные металлические пластины. Подадим в разрыв индуктивности контура 1 переменное напряжение от генератора, см. рис.2а. В витке потечет переменный ток и создаст вокруг проводника магнитное поле. Это сможет подтвердить магнитный индикатор в виде витка, нагруженного лампочкой. Для того, что бы получить открытый колебательный контур, раздвинем пластины конденсатора. Мы наблюдаем, что лампа индикатора магнитного поля продолжает гореть. Чтобы лучше понять, что происходит в данном опыте, смотри рис. 2а. По витку контура 1 течёт ток проводимости, который вокруг себя создает магнитное поле Н, а между пластинами конденсатора – равный ему, так называемый, ток смещения. Несмотря на то, что между пластинами конденсатора нет тока проводимости, опыт показывает, что ток смещения создаёт такое же магнитное поле, как и ток проводимости. Первым, кто об этом догадался, был великий английский физик Дж. К. Максвелл.

В 60-х годах 19-го столетия, формулируя систему уравнений для описания электромагнитных явлений, Дж. К. Максвелл столкнулся с тем, что уравнение для магнитного поля постоянного тока и уравнение сохранения электрических зарядов переменных полей (уравнение непрерывности) несовместимы. Чтобы устранить противоречие, Максвелл, не имея на то никаких экспериментальных данных, постулировал, что магнитное поле порождается не только движением зарядов, но и изменением электрического поля, подобно тому, как электрическое поле порождается не только зарядами, но и изменением магнитного поля. Величину где — электрическая индукция, которую он добавил к плотности тока проводимости, Максвелл назвал током смещения. У электромагнитной индукции появился магнитоэлектрический аналог, а уравнения поля обрели замечательную симметрию. Так, умозрительно был открыт один из фундаментальнейших законов природы, следствием которого является существование электромагнитных волн. В последствии Г.Герц опираясь на эту теорию доказал, что электромагнитное поле излучаемое электрическим вибратором равно полю излучаемое емкостным излучателем.

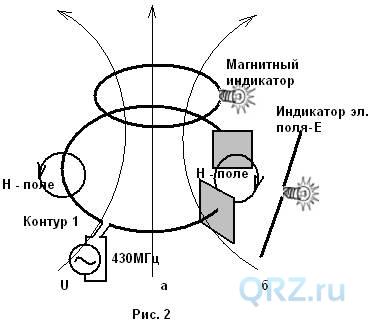
Раз так, убедимся еще раз, что происходит, когда закрытый колебательный контур превращается в открытый и как можно обнаружить электрическое поле Е ? Для этого рядом с колебательным контуром поместим индикатор электрического поля, это вибратор, в разрыв которого включена лампа накаливания, она пока не горит. Постепенно раскрываем контур, и мы наблюдаем, что лампа индикатора электрического поля загорается, рис. 2б. Электрическое поле теперь не сосредоточено между пластинами конденсатора, его силовые линии идут от одной пластины к другой через открытое пространство. Таким образом, мы имеем экспериментальное подтверждение утверждения Дж. К. Максвелла, что емкостной излучатель порождает электромагнитную волну. Никола Тесла обратил на этот факт внимание, что при помощи совсем не больших излучателей можно создать достаточно эффективный прибор для излучения электромагнитной волны. Так родился резонансный трансформатор Н. Тесла. Проверим и этот факт, для чего вновь рассмотрим назначение деталей трансформатора.

И так, сфера и заземление выполняют роль пластин открытого конденсатора. Геометрические размеры сферы и технические данные катушки индуктивности определяют частоту последовательного резонанса, которая должна совпадать с частотой генерации разрядника.

Иными словами, режим последовательного резонанса позволяет трансформатору Тесла достигать таких величин напряжений, что на поверхности сферы появляется коронарный разряд и даже молнии. Весь фокус состоит в том, что коэффициент трансформации резонансного трансформатора выше соотношения витков катушек L1/L2 и значительно выше, чем в трансформаторах с ферро сердечниками. Здесь индуктивность L2, сфера и заземление, представляют из себя открытый резонансный колебательный контур. Именно по этому трансформатор Тесла называется резонансным.

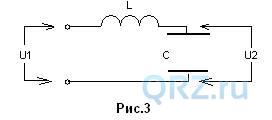
Рассмотрим работу трансформатора Тесла, как последовательный колебательный контур:

— Этот контур необходимо рассматривать как обычный LC – элемент, рис. 1а.б, а так же рис. 2а, где включены последовательно индуктивность L, открытый конденсатор С и сопротивление среды Rср. Угол сдвига фаз в последовательном колебательном контуре между напряжением и током равен нулю (φ=0), если ХL = — Хс, т.е. изменения тока и напряжения в нем происходят синфазно. Это явление называется резонансом напряжений (последовательным резонансом). Следует отметить, что при понижении частоты от резонанса, ток в контуре уменьшается, а резонанс тока несет емкостной характер. При дальнейшей расстройке контура и понижении тока на 0,707, его фаза смещается на 45 градусов. При расстройке контура вверх по частоте, он приобретает индуктивный характер. Это явление часто используют в фазоинверторах.

Если мы рассмотрим схему изображенную на рис. 3, то мы сможем предоставить простые расчеты, из которых видно, что напряжение на пластинах излучателя вычисляется исходя из добротности контура Q, которая реально может находиться в пределах 20 – 50 и много выше.

Где полоса пропускания определяется добротностью контура:

Тогда напряжение на пластинах излучателя будет выглядеть согласно следующей формуле:

В таблице 1 расчетные данные приведены для частоты 7.0 МГц не случайно, это дает возможность любому желающему коротковолновику провести радиолюбительский эксперимент в эфире. Здесь входное напряжение U1 условно взято за 100 Вольт, а добротность за 26.

Источник